题目内容
10.计算(1)$\sqrt{12}$-$\sqrt{18}$+$\root{3}{64}$-|$\sqrt{3}$-4|+$\sqrt{\frac{1}{2}}$;
(2)(3$\sqrt{12}$-2$\sqrt{\frac{1}{3}}$+$\sqrt{48}$)÷2$\sqrt{3}$.
分析 (1)先化二次根式为最简二次根式,再合并同类二次根式即可;
(2)先化二次根式为最简二次根式,再进行除法运算即可.
解答 解:(1)原式=2$\sqrt{3}$-3$\sqrt{2}$+4+$\sqrt{3}$-4+$\frac{\sqrt{2}}{2}$
=$\frac{\sqrt{2}}{2}$;
(2)原式=(6$\sqrt{3}$-$\frac{2\sqrt{3}}{3}$+4$\sqrt{3}$)÷2$\sqrt{3}$
=$\frac{28\sqrt{3}}{3}$×$\frac{1}{2\sqrt{3}}$
=$\frac{14}{3}$.
点评 本题考查了实数的运算,掌握化二次根式为最简二次根式,合并同类二次根式是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图所示,在梯形ABCD中,DC∥AB,$\frac{DC}{AB}$=$\frac{1}{3}$,MN为中位线,EF∥AB且通过AC与BD的交点,点E,F分别在AD,BC上,则梯形CDEF,梯形FEMN,梯形NMAB面积的连比等于5:7:20.
如图所示,在梯形ABCD中,DC∥AB,$\frac{DC}{AB}$=$\frac{1}{3}$,MN为中位线,EF∥AB且通过AC与BD的交点,点E,F分别在AD,BC上,则梯形CDEF,梯形FEMN,梯形NMAB面积的连比等于5:7:20.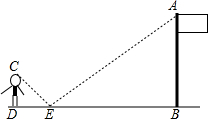 如图,在点E处水平放置一面镜子,人站在D处,恰好能看见旗杆的顶端A,测量眼睛C距地面的高度CD=1.65m,且人与镜子和旗杆底端的距离分别为DE=2m,DB=14.8m.请你计算出旗杆的高度.
如图,在点E处水平放置一面镜子,人站在D处,恰好能看见旗杆的顶端A,测量眼睛C距地面的高度CD=1.65m,且人与镜子和旗杆底端的距离分别为DE=2m,DB=14.8m.请你计算出旗杆的高度.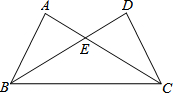 如图,在△ABC与△DCB中,AC与BD交于点E,且∠A=∠D=90°,AB=DC.
如图,在△ABC与△DCB中,AC与BD交于点E,且∠A=∠D=90°,AB=DC.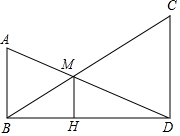 如图,AB和CD表示两根立于地面的柱子,AD和BC表示起固定作用的两根钢筋,AD与BC的交点为M.已知AB=10m,CD=15m,则点M离地面的高度MH=6m.
如图,AB和CD表示两根立于地面的柱子,AD和BC表示起固定作用的两根钢筋,AD与BC的交点为M.已知AB=10m,CD=15m,则点M离地面的高度MH=6m.