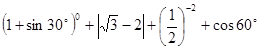题目内容
已知:关于x的一元二次方程 (k是整数).
(k是整数).
(1)求证:方程有两个不相等的实数根;
(2)若方程的两个实数根分别为x1,x2(其中x1<x2),设 ,判断y是否为变量k的函数?如果是,请写出函数解析式;若不是,请说明理由.
,判断y是否为变量k的函数?如果是,请写出函数解析式;若不是,请说明理由.
 (k是整数).
(k是整数).(1)求证:方程有两个不相等的实数根;
(2)若方程的两个实数根分别为x1,x2(其中x1<x2),设
 ,判断y是否为变量k的函数?如果是,请写出函数解析式;若不是,请说明理由.
,判断y是否为变量k的函数?如果是,请写出函数解析式;若不是,请说明理由.(1)见解析(2)y是为变量k的函数
解:(1)证明:方程 是一元二次方程,∴k≠0。
是一元二次方程,∴k≠0。
 ,
,
∵k是整数,∴k≠ ,2k-1≠0,
,2k-1≠0,
∴ >0。∴方程有两个不相等的实数根。
>0。∴方程有两个不相等的实数根。
(2)y是k的函数。
解方程得 ,∴x=3或x=
,∴x=3或x= 。
。
∵k是整数,∴ ≤1。∴
≤1。∴ ≤2<3。
≤2<3。
又∵x1<x2,∴x1= ,x2=3。
,x2=3。
∴ 。
。
∴y是为变量k的函数。
(1)根据一元二次方程定义得k≠0,再计算△得 ,而k是整数,则2k-1≠0,得到△>0,根据△的意义即可得到方程有两个不相等的实数根。
,而k是整数,则2k-1≠0,得到△>0,根据△的意义即可得到方程有两个不相等的实数根。
(2)先根据求根公式求出一元二次方程 的解为x=3或x=
的解为x=3或x= ,而k是整数,x1<x2,则有x1=
,而k是整数,x1<x2,则有x1= ,x2=3,代入得到
,x2=3,代入得到 即可得出结论。
即可得出结论。
 是一元二次方程,∴k≠0。
是一元二次方程,∴k≠0。 ,
,∵k是整数,∴k≠
 ,2k-1≠0,
,2k-1≠0,∴
 >0。∴方程有两个不相等的实数根。
>0。∴方程有两个不相等的实数根。(2)y是k的函数。
解方程得
 ,∴x=3或x=
,∴x=3或x= 。
。∵k是整数,∴
 ≤1。∴
≤1。∴ ≤2<3。
≤2<3。又∵x1<x2,∴x1=
 ,x2=3。
,x2=3。∴
 。
。∴y是为变量k的函数。
(1)根据一元二次方程定义得k≠0,再计算△得
 ,而k是整数,则2k-1≠0,得到△>0,根据△的意义即可得到方程有两个不相等的实数根。
,而k是整数,则2k-1≠0,得到△>0,根据△的意义即可得到方程有两个不相等的实数根。(2)先根据求根公式求出一元二次方程
 的解为x=3或x=
的解为x=3或x= ,而k是整数,x1<x2,则有x1=
,而k是整数,x1<x2,则有x1= ,x2=3,代入得到
,x2=3,代入得到 即可得出结论。
即可得出结论。
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 ,且a≠b,则
,且a≠b,则 的值是【 】
的值是【 】 有两个不相等的实数根.
有两个不相等的实数根. 的方程
的方程 有两个不等的实数根,则实数
有两个不等的实数根,则实数 的取值范围为 ( )
的取值范围为 ( )

 且
且
 且
且 2
2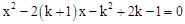 的根的情况为
的根的情况为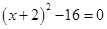 (2)
(2)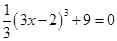
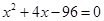 ; (2) 计算:
; (2) 计算: