题目内容
【题目】如图,在平面直角坐标系中,一次函数![]() 的图像与反比例函数
的图像与反比例函数![]() 的图像相交于点
的图像相交于点![]() ,一次函数
,一次函数![]() 与
与![]() 轴相交于点
轴相交于点![]() ,与
,与![]() 轴相交于点
轴相交于点![]() .
.
(1)求![]() 和
和![]() 的值;
的值;
(2)点![]() 在
在![]() 轴正半轴上,且
轴正半轴上,且![]() 的面积为1,求点
的面积为1,求点![]() 坐标;
坐标;
(3)在(2)的条件下,点![]() 是一次函数
是一次函数![]() 上一点,点
上一点,点![]() 是反比例函数
是反比例函数![]() 图像上一点,且点
图像上一点,且点![]() 、
、![]() 都在
都在![]() 轴上方.如果以
轴上方.如果以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形为平行四边形,请直接写出点
为顶点的四边形为平行四边形,请直接写出点![]() 、
、![]() 的坐标.
的坐标.

【答案】(1)1,1;(2)![]() ;(3)
;(3)![]() ,
,![]() 或
或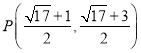 ,
,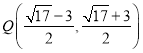 .
.
【解析】
(1)将B与C坐标代入一次函数解析式即可求出k与b的值;
(2)先求出点A的坐标,设点M的坐标为![]() ,再根据
,再根据![]() 的面积为1列出方程求出m的值进而得解;
的面积为1列出方程求出m的值进而得解;
(3)由题意可得PQ∥BM且PQ=BM=2,设点P(a+2,a+1),则可表示点Q的坐标,利用点Q在反比例函数图像上列出方程求解即可.
解:(1)把点![]() ,
,![]() ,代入函数
,代入函数![]() 得,
得,
由题意得![]() 解得
解得![]()
(2)由题意得,点![]() 在一次函数
在一次函数![]() 和反比例函数
和反比例函数![]() 上,
上,
则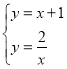 ,
,
化简得,![]() ,解得
,解得![]() ,
,![]() ,
,
因为点![]() 在第一象限所以
在第一象限所以![]()
所以点![]() 坐标为
坐标为![]()
设:![]() 点坐标为
点坐标为![]()
则![]() ,
,
![]()
解得,![]() .
.
![]() 点坐标为
点坐标为![]()
(3)由(2)得,点M为![]()
又∵![]()
∴BM=2,
∵以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形为平行四边形,且点
为顶点的四边形为平行四边形,且点![]() 、
、![]() 都在
都在![]() 轴上方,
轴上方,
∴PQ∥BM且PQ=BM=2,
设点P(a,a+1),
当点Q在点P右侧时,则点Q为(a+2,a+1)
将(a+2,a+1)代入![]() 得
得
(a+2)(a+1)=2
解得,a=0或a=-3(舍去)
∴![]() ,
,![]()
当点Q在点P左侧时,则点Q为(a-2,a+1)
将(a-2,a+1)代入![]() 得
得
(a-2)(a+1)=2
解得,a=![]() 或a=
或a=![]() (舍去)
(舍去)
∴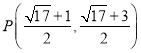 ,
,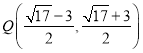 .
.
∴![]() ,
,![]() 或
或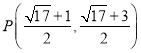 ,
,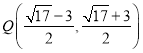 .
.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目