题目内容
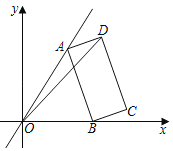
【题目】如图,在平面直角坐标系中,点A在一次函数y=![]() x位于第一象限的图象上运动,点B在x轴正半轴上运动,在AB右侧以它为边作矩形ABCD,且AB=2
x位于第一象限的图象上运动,点B在x轴正半轴上运动,在AB右侧以它为边作矩形ABCD,且AB=2![]() ,AD=1,则OD的最大值是( )
,AD=1,则OD的最大值是( )
A.![]() B.
B.![]() +2C.
+2C.![]() +2D.
+2D.![]()
【答案】B
【解析】
作△AOB的外接圆⊙P,连接OP、PA、PB、PD,作PG⊥CD,交AB于H,垂足为G,易得∠APH=∠AOB,解直角三角形求得PH=2,然后根据三角形三边关系得出OD取最大值时,OD=OP+PD,据此即可求得.
解:∵点A在一次函数y=![]() x图象上,∴tan∠AOB=
x图象上,∴tan∠AOB=![]() ,
,
作△AOB的外接圆⊙P,连接OP、PA、PB、PD,作PG⊥CD,交AB于H,垂足为G,

∵四边形ABCD是矩形,
∴AB∥CD,四边形AHGD是矩形,
∴PG⊥AB,GH=AD=1,
∵∠APB=2∠AOB,∠APH=![]() ∠APB,AH=
∠APB,AH=![]() AB=
AB=![]() =DG,
=DG,
∴∠APH=∠AOB,
∴tan∠APH=tan∠AOB=![]() ,
,
∴![]() =
=![]() ,
,
∴PH=1,
∴PG=PH+HG=1+1=2,
∴PD=![]() =
=![]() =
=![]() ,
,
∴OP=PA=![]() =
=![]() =2,
=2,
在△OPD中,OP+PD≥OD,
∴OD的最大值为:OP+PD=2+![]() ,
,
故选:B.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目