题目内容
 已知,AB是⊙O的直径,BC⊥AB,过点C作⊙O的切线CE,点D是CE延长线上一点,连AD,且AD+BC=CD.
已知,AB是⊙O的直径,BC⊥AB,过点C作⊙O的切线CE,点D是CE延长线上一点,连AD,且AD+BC=CD.(1)求证:AD是⊙O的切线;
(2)设OE交AC于F,若OF=3,EF=2,求线段BC的长.
考点:切线的判定
专题:
分析:(1)如图,作辅助线,证明△AOD≌△EOD,进而得到∠DAO=∠DEO=90°,即可解决问题.
(2)如图,作辅助线,证明△AEF∽△COF,进而证明CF:AF=OF:EF=3:2,根据勾股定理,结合其他知识即可解决问题.
(2)如图,作辅助线,证明△AEF∽△COF,进而证明CF:AF=OF:EF=3:2,根据勾股定理,结合其他知识即可解决问题.
解答: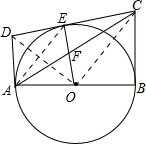 解:(1)如图,连接OD;
解:(1)如图,连接OD;
∵BC⊥AB,且AB是⊙O的直径,
∴BC是⊙O的切线;而DC是⊙O的切线,
∴CB=CE;DC⊥OE;
∵AD+BC=CD,
∴AD=ED;在△AOD与△EOD中,
,
∴△AOD≌△EOD(SSS),
∴∠DAO=∠DEO=90°,
∴AD是⊙O的切线.
(2)如图,连接AE、OC;
∵CB、CE均为⊙O的切线,
∴∠ECO=∠BCO,BC=EC(设为μ);
∴∠EOC=∠BOC=
;
∵OA=OE,
∴∠OAE=∠OEA=
,
∴ ∠OEA=∠EOC,
∠OEA=∠EOC,
∴AE∥OC,△AEF∽△COF,
∴CF:AF=OF:EF=3:2,
设CF=3λ,则AF=2λ,AC=5λ;
由勾股定理得:CF2=22+μ2,AC2=102+μ2,
∴(
)2=
,
解得μ=5
,
即线段BC的长为5
.
 解:(1)如图,连接OD;
解:(1)如图,连接OD;∵BC⊥AB,且AB是⊙O的直径,
∴BC是⊙O的切线;而DC是⊙O的切线,
∴CB=CE;DC⊥OE;
∵AD+BC=CD,
∴AD=ED;在△AOD与△EOD中,
|
∴△AOD≌△EOD(SSS),
∴∠DAO=∠DEO=90°,
∴AD是⊙O的切线.
(2)如图,连接AE、OC;
∵CB、CE均为⊙O的切线,
∴∠ECO=∠BCO,BC=EC(设为μ);
∴∠EOC=∠BOC=
| 180°-∠AOE |
| 2 |
∵OA=OE,
∴∠OAE=∠OEA=
| 180°-∠AOE |
| 2 |
∴
 ∠OEA=∠EOC,
∠OEA=∠EOC,∴AE∥OC,△AEF∽△COF,
∴CF:AF=OF:EF=3:2,
设CF=3λ,则AF=2λ,AC=5λ;
由勾股定理得:CF2=22+μ2,AC2=102+μ2,
∴(
| 3λ |
| 5λ |
| μ2+4 |
| μ2+100 |
解得μ=5
| 2 |
即线段BC的长为5
| 2 |
点评:该题主要考查了切线的判定及其性质的应用问题;解题的关键是灵活运用有关定理来分析、判断、推理或解答;对综合运用能力提出了较高的要求.

练习册系列答案
相关题目
4°32′35″×6的结果为( )
| A、28°27′30″ |
| B、27°15′30″ |
| C、24°200′ |
| D、24°32′35″ |
化简
+
的结果是( )
| x2 |
| x-y |
| y2 |
| y-x |
| A、-x-y | B、y-x |
| C、x-y | D、x+y |

 如图,在矩形ABCD中,BC沿EF对折,与AD重合,P是BC边上动点,DP与EF交于点G.
如图,在矩形ABCD中,BC沿EF对折,与AD重合,P是BC边上动点,DP与EF交于点G. 如图,AD是△ABC的中线,EF∥BC,分别与AB、AC、AD相交于点E、F、G.判断EG与FG是否相等,并说明理由.
如图,AD是△ABC的中线,EF∥BC,分别与AB、AC、AD相交于点E、F、G.判断EG与FG是否相等,并说明理由.