题目内容
若直角三角形两直角边长之比为3:4,斜边为10,则它的面积是 .
考点:勾股定理
专题:
分析:设直角三角形两直角边长分别为3x,4x,再根据勾股定理求出x的值,进而得出结论.
解答:解:∵直角三角形两直角边长之比为3:4,
∴设直角三角形两直角边长分别为3x,4x,
∵斜边为10,
∴
=10,解得x=2,
∴两直角分别为6,8,
∴它的面积=
×6×8=24.
故答案为:24.
∴设直角三角形两直角边长分别为3x,4x,
∵斜边为10,
∴
| (3x)2+(4x)2 |
∴两直角分别为6,8,
∴它的面积=
| 1 |
| 2 |
故答案为:24.
点评:本题考查的是勾股定理,熟知在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键.

练习册系列答案
相关题目
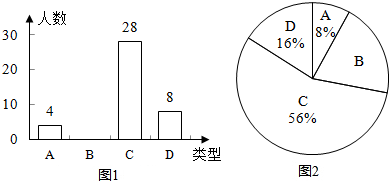
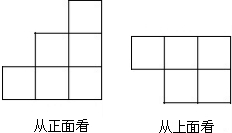 用小立方块搭一个几何体,如图是从正面和上面看到的几何体的形状图,搭成过样的几何体最少需多少个小立方块?最多需要多少个立方块?并画出需要最多立方块时从左面看到的几何体的形状图.
用小立方块搭一个几何体,如图是从正面和上面看到的几何体的形状图,搭成过样的几何体最少需多少个小立方块?最多需要多少个立方块?并画出需要最多立方块时从左面看到的几何体的形状图. 如图,一张长为4,宽为3的长方形纸片ABCD,沿对角线BD对折,点C落在点E的位置,BE交AD于G,求AG的长.
如图,一张长为4,宽为3的长方形纸片ABCD,沿对角线BD对折,点C落在点E的位置,BE交AD于G,求AG的长.
 如图,在Rt△ABC中,∠C=90°,∠A=30°,BC=14cm,点P从点B出发,沿BA方向以每秒2cm的速度向终点A运动;同时,动点Q从点C出发沿CB方向以每秒1.5cm的速度向终点B运动,将△BPQ沿BC翻折,点P的对应点为点P′,设点P、Q运动的时间为t秒,要使四边形BPQP′为菱形,则t的值为( )
如图,在Rt△ABC中,∠C=90°,∠A=30°,BC=14cm,点P从点B出发,沿BA方向以每秒2cm的速度向终点A运动;同时,动点Q从点C出发沿CB方向以每秒1.5cm的速度向终点B运动,将△BPQ沿BC翻折,点P的对应点为点P′,设点P、Q运动的时间为t秒,要使四边形BPQP′为菱形,则t的值为( )