题目内容
 如图,在等腰直角三角形ABC中,∠C=90°,长方形DEFG的各顶点都在三角形ABC的边上,已知CD与DA的长度比为3:2,长方形DEFG的面积为36cm2,则△ABC的面积是( )
如图,在等腰直角三角形ABC中,∠C=90°,长方形DEFG的各顶点都在三角形ABC的边上,已知CD与DA的长度比为3:2,长方形DEFG的面积为36cm2,则△ABC的面积是( )分析:设长方形DEFG中DG=x,GF=DE=y,由条件表示出DC=
x,AD=
y,再由条件建立方程组就可以x、y的值,从而求出AC的值,进而求出△ABC的面积.
| ||
| 2 |
| 2 |
解答:解:设长方形DEFG的DG=x,GF=DE=y,
∴xy=36,
∵四边形DEFG是矩形,
∴DG∥AB,
∴∠CDG=∠CAB,∠CGD=∠CBA.
∵三角形ABC是等腰直角三角形,∠C=90°,
∴∠A=∠B=45°,
∴∠CDG=∠CGD=45°,由勾股定理,得
∴DC=
x,AD=
y,
∵CD:DA=3:2,
∴
=
=
,
∴x:2y=3:2,
,
解得
,
∴DC=3
,AD=2
,
∴AC=5
,
∴S△ABC=
=75.
∴故选A.
∴xy=36,
∵四边形DEFG是矩形,
∴DG∥AB,
∴∠CDG=∠CAB,∠CGD=∠CBA.
∵三角形ABC是等腰直角三角形,∠C=90°,
∴∠A=∠B=45°,
∴∠CDG=∠CGD=45°,由勾股定理,得
∴DC=
| ||
| 2 |
| 2 |
∵CD:DA=3:2,
∴
| CD |
| DA |
| ||||
|
| 3 |
| 2 |
∴x:2y=3:2,
|
解得
|
∴DC=3
| 6 |
| 6 |
∴AC=5
| 6 |
∴S△ABC=
5
| ||||
| 2 |
∴故选A.
点评:本题考查了矩形的性质,勾股定理的运用,由题意列方程组和求方程组的解的方法,等腰直角三角形的性质,三角形的面积公式的运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
教材中第25章锐角的三角比,在这章的小结中有如下一段话:锐角三角比定量地描述了在直角三角形中边角之间的联系.在直角三角形中,一个锐角的大小与两条边长的比值相互唯一确定,因此边长与角的大小之间可以相互转化.
类似的,可以在等腰三角形中建立边角之间的联系,我们定义:等腰三角形中底边与腰的比叫做顶角的正对(sad).如图,在△ABC中,AB=AC,顶角A的正对记作sadA,这时
sad A= .容易知道一个角的大小与这个角的正对值也是相互唯一确定的.
.容易知道一个角的大小与这个角的正对值也是相互唯一确定的.
根据上述对角的正对定义,解下列问题:

(1)sad 的值为( ▼ )
的值为( ▼ )
(2)对于 ,∠A的正对值sad A的取值范围是 ▼ .
,∠A的正对值sad A的取值范围是 ▼ .
(3)已知 ,其中
,其中 为锐角,试求sad
为锐角,试求sad 的值.
的值.
类似的,可以在等腰三角形中建立边角之间的联系,我们定义:等腰三角形中底边与腰的比叫做顶角的正对(sad).如图,在△ABC中,AB=AC,顶角A的正对记作sadA,这时
sad A=
 .容易知道一个角的大小与这个角的正对值也是相互唯一确定的.
.容易知道一个角的大小与这个角的正对值也是相互唯一确定的.根据上述对角的正对定义,解下列问题:

(1)sad
 的值为( ▼ )
的值为( ▼ )A. | B.1 | C. | D.2 |
 ,∠A的正对值sad A的取值范围是 ▼ .
,∠A的正对值sad A的取值范围是 ▼ .(3)已知
 ,其中
,其中 为锐角,试求sad
为锐角,试求sad 的值.
的值. 教材中第25章锐角的三角比,在这章的小结中有如下一段话:锐角三角比定量地描述了在直角三角形中边角之间的联系.在直角三角形中,一个锐角的大小与两条边长的比值相互唯一确定,因此边长与角的大小之间可以相互转化.
类似的,可以在等腰三角形中建立边角之间的联系,我们定义:等腰三角形中底边与腰的比叫做顶角的正对(sad).如图,在△ABC中,AB=AC,顶角A的正对记作sadA,这时
sad A= .容易知道一个角的大小与这个角的正对值也是相互唯一确定的.
.容易知道一个角的大小与这个角的正对值也是相互唯一确定的.
根据上述对角的正对定义,解下列问题:
(1)sad  的值为( ▼ )
的值为( ▼ )
A. | B.1 | C. | D.2 |
 ,∠A的正对值sad A的取值范围是 ▼ .
,∠A的正对值sad A的取值范围是 ▼ .(3)已知
 ,其中
,其中 为锐角,试求sad
为锐角,试求sad 的值.
的值. 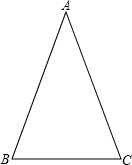 互唯一确定的.
互唯一确定的.
 .容易知道一个角的大小与这个角的正对值也是相互唯一确定的.
.容易知道一个角的大小与这个角的正对值也是相互唯一确定的.
 的值为( ▼ )
的值为( ▼ ) B.
1 C.
B.
1 C.  D.
2
D.
2 ,∠A的正对值sad A的取值范围是 ▼ .
,∠A的正对值sad A的取值范围是 ▼ . ,其中
,其中 为锐角,试求sad
为锐角,试求sad