题目内容
如图， 
△ABC内接于⊙O，CA=CB，CD∥AB且与OA的延长线交于点D.
(1)判断CD与⊙O的位置关系，并说明理由；
(2)若∠ACB=120°，OA=2，求CD的长．
解: (1) CD与⊙O的位置关系是相切.理由如下：
如图，作直径CE，连接AE．
∵ CE是直径，∴ ∠
90°，∴ ∠
∠
90°.
∵ 
B，∴ ∠
∠
.
∵ AB∥CD，∴ ∠
∠. ∵ ∠∠
，∴ ∠∠，
∴ ∠
∠
90°，即∠
90°，
∴ OC⊥DC，∴ CD与⊙O相切．
（2）∵ CD∥AB，OC⊥DC，∴ OC⊥AB.
又∠
120°，∴ ∠
∠
60°.
∵ 
，∴ △OAC是等边三角形，∴ ∠
60°.
在Rt△DCO中，
，
∴ 
．
练习册系列答案
相关题目
5、如图，△ABC内接于⊙O，∠C=30°，AB=5，则⊙O的直径为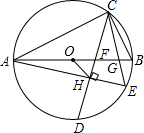
如图，△ABC内接于⊙O，AB是⊙O的直径，CD平分∠ACB交⊙O于点D，交AB于点F，弦AE⊥CD于点H，连接CE、OH．
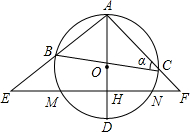
na=
（2012•南昌模拟）如图，△ABC内接于⊙O，点D在OC的延长线上，已知：∠B=∠CAD=30°．
（2012•密云县一模）如图，△ABC内接于⊙O，AB是⊙O的直径，∠ABC=20°，点D是弧CAB上一点，若∠ABC=20°，则∠D的度数是