Question

【题目】如图，将长方形 ABCD 沿 EF 折叠，使点 D 与点 B 重合．

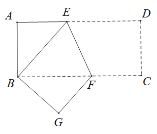
（1）若∠AEB=40°，求∠BFE 的度数；

（2）若 AB=6，AD=18，求 CF 的长．

Answer 1

【答案】（1）70°； （2）8．

【解析】

（1）依据平行线的性质可求得∠BFE=∠FED，然后依据翻折的性质可求得∠BEF=∠DEF，最后根据平角的定义可求得∠BFE的度数;

（2）先依据翻折的性质得到CF=GF,AB=DC=BG=6，然后设CF=GF=x，然后在RT△BGF中，依据勾股定理列出关于x的方程求解即可．

解：（1）∵AD∥BC，

∴∠BFE=∠FED，

由翻折的性质可知：∠BEF=∠DEF，

∴∠BFE=∠FED=∠BEF

∵∠FED＋∠BEF＋∠AEB=180°

∴2∠BFE =180°-40°=140°，

∴∠BFE=70°;

（2）由翻折的性质可知CF=GF,AB=DC=BG=6,

设CF=GF=x，则BF=18-x,

在Rt△BGF中，依据勾股定理可知：BF2=BG2+GF2，

即(18-x)2=62+x2，

解得：x=8

即CF=8