题目内容
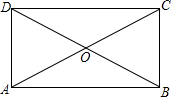 如图,点O是矩形ABCD的两对角线的交点,已知∠COD=120°,AC=10cm.
如图,点O是矩形ABCD的两对角线的交点,已知∠COD=120°,AC=10cm.求矩形ABCD的面积.
分析:根据矩形的对角线相等且互相平分可得OA=OD,BD=AC,然后求出△AOD是等边三角形,再根据等边三角形的性质求出AD,再利用勾股定理列式求出AB,然后利用矩形的面积公式列式进行计算即可得解.
解答:解:在矩形ABCD中,OA=OD,BD=AC=10cm,
∵∠COD=120°,
∴∠AOD=180°-120°=60°,
∴△AOD的等边三角形,
∴AD=OA=
AC=
×10=5cm,
根据勾股定理,AB=
=
=5
cm,
所以,S=
•AB•AD=
×5
×5=
cm2.
∵∠COD=120°,
∴∠AOD=180°-120°=60°,
∴△AOD的等边三角形,
∴AD=OA=
| 1 |
| 2 |
| 1 |
| 2 |
根据勾股定理,AB=
| BD2-AD2 |
| 102-52 |
| 3 |
所以,S=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
25
| ||
| 2 |
点评:本题考查了矩形的性质,勾股定理的应用,主要利用了矩形的对角线相等且互相平分的性质,等边三角形的判定与性质,求出矩形的长与宽是解题的关键.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
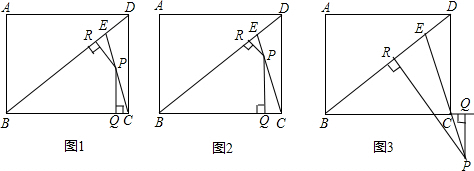
 12、如图,点E是矩形ABCD中BC边的中点,AB=6,当AE⊥DE时,矩形ABCD的周长是( )
12、如图,点E是矩形ABCD中BC边的中点,AB=6,当AE⊥DE时,矩形ABCD的周长是( ) 如图,点O是矩形ABCD的中心,E是AB上的点,沿CE折叠后,点B恰好与点O重合.若BC=3,则折痕CE的长为
如图,点O是矩形ABCD的中心,E是AB上的点,沿CE折叠后,点B恰好与点O重合.若BC=3,则折痕CE的长为 (2013•宝应县一模)如图,点O是矩形ABCD的中心,E是AB上的点,沿CE折叠后,点B恰好与点O重合,若BC=3,求折痕CE的长.
(2013•宝应县一模)如图,点O是矩形ABCD的中心,E是AB上的点,沿CE折叠后,点B恰好与点O重合,若BC=3,求折痕CE的长. 如图,点P是矩形ABCD对角线BD上的一个动点,AB=6,AD=8,则PA+PC的最小值为
如图,点P是矩形ABCD对角线BD上的一个动点,AB=6,AD=8,则PA+PC的最小值为