题目内容
12.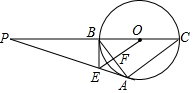 如图,△ABC内接于⊙O,BC是直径,⊙O的切线PA交CB的延长线于点P,OE∥AC交AB于点F,交PA于点E,连接BE.
如图,△ABC内接于⊙O,BC是直径,⊙O的切线PA交CB的延长线于点P,OE∥AC交AB于点F,交PA于点E,连接BE.(1)判断BE与⊙O的位置关系并说明理由;
(2)若⊙O的半径为8,BE=6,求AB的长.
分析 (1)结论:BE是⊙O的切线.首先证明∠OAP=90°,再证明△EOB≌△EOA,推出∠OBE=∠OAE即可解决问题.
(2)由(1)可知AB=2BF,在Rt△BEO中,∠OBE=90°,OB=8,BE=6,可得OE=$\sqrt{B{E}^{2}+O{B}^{2}}$=10,由$\frac{1}{2}$•BE•OB=$\frac{1}{2}$•OE•BF,可得BF=$\frac{6×8}{10}$=$\frac{12}{5}$,由此即可解决问题.
解答 解:(1)BE是⊙O的切线.
理由:如图连接OA.
∵PA是切线,
∴PA⊥OA,
∴∠OAP=90°,
∵BC是直径,
∴∠BAC=90°,
∵OE∥AC,
∴∠OFB=∠BAC=90°,
∴OE⊥AB,
∴BF=FA,
∵OB=OA,
∴∠EOB=∠EOA,
在△EOB和△EOA中,
$\left\{\begin{array}{l}{EO=OA}\\{∠EOB=∠EOA}\\{OE=OE}\end{array}\right.$,
∴△EOB≌△EOA,
∴∠OBE=∠OAE=90°,
∴OB⊥BE,
∴BE是⊙O的切线.
(2)由(1)可知AB=2BF,
在Rt△BEO中,∵∠OBE=90°,OB=8,BE=6,
∴OE=$\sqrt{B{E}^{2}+O{B}^{2}}$=10,
∵$\frac{1}{2}$•BE•OB=$\frac{1}{2}$•OE•BF,
∴BF=$\frac{6×8}{10}$=$\frac{12}{5}$,
∴AB=2BF=$\frac{24}{5}$.
点评 本题考查切线的性质、垂径定理、等腰三角形的性质、全等三角形的判定和性质、勾股定理等知识,解题的关键是灵活运用所学知识,学会利用面积法求线段的长,属于中考常考题型.

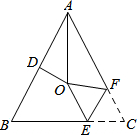 如图,△ABC中,AB=AC,∠BAC=54°,∠BAC的平分线与AB的垂直平分线交于点O,将∠C沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合,则∠OEC的度数是( )
如图,△ABC中,AB=AC,∠BAC=54°,∠BAC的平分线与AB的垂直平分线交于点O,将∠C沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合,则∠OEC的度数是( )| A. | 106° | B. | 108° | C. | 110° | D. | 112° |
 一次函数y=kx-4的图象如图所示,则k的取值范围是( )
一次函数y=kx-4的图象如图所示,则k的取值范围是( )| A. | k>1 | B. | k>0 | C. | k<0 | D. | k=0 |
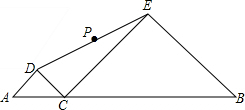 如图,线段AB长为6,点C是线段AB上一动点(不与A,B重合)分别以AC和BC为斜边,在AB的同侧作等腰直角三角形△ADC,△CEB,点P是DE的中点,当点C从距离A点1处沿AB向右运动至距离B点1处时,点P运动的路径长是2.
如图,线段AB长为6,点C是线段AB上一动点(不与A,B重合)分别以AC和BC为斜边,在AB的同侧作等腰直角三角形△ADC,△CEB,点P是DE的中点,当点C从距离A点1处沿AB向右运动至距离B点1处时,点P运动的路径长是2.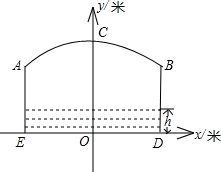 如图,小河上有一拱桥,拱桥及河道的截面轮廓线由抛物线的一部分ACB和矩形的三边AE、ED、DB组成,已知河底ED是水平的,ED=16米,AE=8米,抛物线的顶点C到ED的距离是11米,以ED所在的直线为x轴,抛物线的对称轴为y轴建立平面直角坐标系.
如图,小河上有一拱桥,拱桥及河道的截面轮廓线由抛物线的一部分ACB和矩形的三边AE、ED、DB组成,已知河底ED是水平的,ED=16米,AE=8米,抛物线的顶点C到ED的距离是11米,以ED所在的直线为x轴,抛物线的对称轴为y轴建立平面直角坐标系.
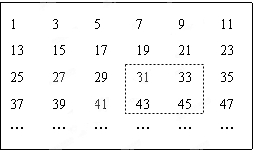 将连续的奇数1,3,5,7,9…排成如图所示的数表,用长方形框选其中的四个数.
将连续的奇数1,3,5,7,9…排成如图所示的数表,用长方形框选其中的四个数.