题目内容
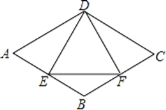
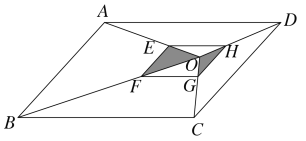
【题目】如图,四边形ABCD,EFGH都是平行四边形,点O是![]() 内的一点,点E、F、G,H分别是OA、OB、OC、OD上的一点,EF //AB,OA= 3OE,若阴影部分的面积为S,则
内的一点,点E、F、G,H分别是OA、OB、OC、OD上的一点,EF //AB,OA= 3OE,若阴影部分的面积为S,则![]() 的面积为( )
的面积为( )
A.6SB.18SC.24SD.32S
【答案】B
【解析】
过O点作OM⊥AB于点M,延长MO与CD交于点N,易得ON⊥CD,由平行四边形面积公式和三角形面积公式可推出S△OAB+S△OCD=![]()
![]() ,再由相似三角形面积比等于相似比的平方可得S△OEF=
,再由相似三角形面积比等于相似比的平方可得S△OEF=![]() S△OAB,S△OGH=
S△OAB,S△OGH=![]() S△OCD,进而得出阴影部分面积与
S△OCD,进而得出阴影部分面积与![]() 面积之间的关系,即可得出答案.
面积之间的关系,即可得出答案.
如图,过O点作OM⊥AB于点M,延长MO与CD交于点N,

∵四边形ABCD是平行四边形
∴AB∥CD,AB=CD
∴ON⊥CD
∵S△OAB=![]() ,S△OCD=
,S△OCD=![]()
![]() ,
,![]()
∴S△OAB+S△OCD=![]() =
=![]()
![]()
∵EF∥AB
∴△OEF∽△OAB,
∴![]() ,
,
∴ ,即S△OEF=
,即S△OEF=![]() S△OAB,
S△OAB,
∵四边形EFGH是平行四边形
∴EF∥GH,EF=GH
又∵EF∥AB,AB∥CD
∴GH∥CD
∴△OGH∽△OCD,
∴ ,即S△OGH=
,即S△OGH=![]() S△OCD,
S△OCD,
∴阴影部分面积S=S△OEF+S△OGH=![]() ,
,
∴![]()
故选B.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目