题目内容
20.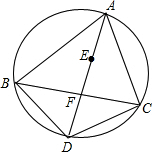 已知,如图,在△ABC中,E是内心,延长AE交△ABC的外接圆于点D,弦AD交弦BC于点F.
已知,如图,在△ABC中,E是内心,延长AE交△ABC的外接圆于点D,弦AD交弦BC于点F.(1)求证:DE=DB;
(2)若cos∠BAC=$\frac{1}{2}$,BC=6,则DE=2$\sqrt{3}$.
分析 (1)由三角形内心的定义可知∠1=∠4,∠2=∠3,由同弧所对的圆周角相等可知:∠4=∠5,于是可得到∠1+∠2=∠3+∠5,即∠BED=∠EBD,故此可证得DE=DB;
(2))由cos∠BAC=$\frac{1}{2}$,从而得到∠BAC=60°,由E是△ABC的内心,可知∠BAD=∠CAD=30°,于是可证得∠CBD=∠BCD=30°,从而得到BD=DC,由等腰三角形三线合一的性质可知:BG=CG=3,最后依据特殊锐角三角函数值可求得BD的长.
解答 解:(1)连接BE.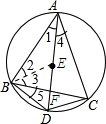
∵在△ABC中,E是内心,
∴∠1=∠4,∠2=∠3.
又∵∠4=∠5,
∴∠1+∠2=∠3+∠4=∠3+∠5.
∴∠BED=∠EBD.
∴DE=DB.
(2)过点D作DG⊥BC,垂足为G.
∵cos∠BAC=$\frac{1}{2}$,
∴∠BAC=60°.
∵E是△ABC的内心,
∴∠BAD=∠CAD=30°.
∴∠CBD=∠BCD=30°.
∴BD=DC.
又∵DG⊥BC,
∴BG=CG=3.
∴BD=$\frac{BG}{cos30°}$=$\frac{3}{\frac{\sqrt{3}}{2}}$=2$\sqrt{3}$.
故答案为:2$\sqrt{3}$.
点评 本题主要考查的是三角形的内心、特殊锐角三角函数值、等腰三角形、等边三角形的性质和判定,证得△BDC为等腰直角三角形是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.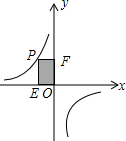 如图,P是反比例函数图象在第二象限上的一点,且矩形PEOF的面积为5.这个函数的解析式为( )
如图,P是反比例函数图象在第二象限上的一点,且矩形PEOF的面积为5.这个函数的解析式为( )
 如图,P是反比例函数图象在第二象限上的一点,且矩形PEOF的面积为5.这个函数的解析式为( )
如图,P是反比例函数图象在第二象限上的一点,且矩形PEOF的面积为5.这个函数的解析式为( )| A. | y=$\frac{5}{x}$ | B. | y=-$\frac{5}{x}$ | C. | y=$\frac{10}{x}$ | D. | y=-$\frac{x}{5}$ |
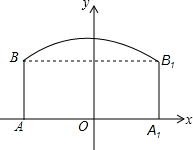 如图,隧道的截面由抛物线和长方形构成,长方形的长为16m,宽为6m,抛物线的最高点C离地面AA1的距离为8m.
如图,隧道的截面由抛物线和长方形构成,长方形的长为16m,宽为6m,抛物线的最高点C离地面AA1的距离为8m.