题目内容
14．
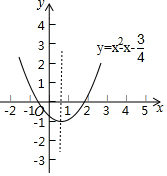如图，根据函数y=x2-x-$\frac{3}{4}$的图象填空：（1）图象与x轴交点的坐标是（-$\frac{1}{2}$，0），（$\frac{3}{2}$，0）．
（2）当x=-$\frac{1}{2}$或$\frac{3}{2}$时，y=0；方程x2-x-$\frac{3}{4}$=0的解是x1=-$\frac{1}{2}$，x2=$\frac{3}{2}$
（3）当x取-$\frac{1}{2}$＜x＜$\frac{3}{2}$时，y＜0；当x取x＜-$\frac{1}{2}$或x＞$\frac{3}{2}$时，y＞0
（4）x2-x-$\frac{3}{4}$＜0的解集是-$\frac{1}{2}$＜x＜$\frac{3}{2}$，x2-x-$\frac{3}{4}$＞0的解集是x＜-$\frac{1}{2}$或x＞$\frac{3}{2}$．
分析 （1）令y=0，解关于x的一元二次方程，然后写出与x轴的交点坐标即可；
（2）根据（1）的求解结果解答即可；
（3）根据函数图象分别写出x轴下方和上方部分的x的取值范围即可；
（4）根据（3）的结论解答即可．
解答 解：（1）令y=0，则x2-x-$\frac{3}{4}$=0，
解得x1=-$\frac{1}{2}$，x2=$\frac{3}{2}$，
所以，图象与x轴的交点坐标为（-$\frac{1}{2}$，0），（$\frac{3}{2}$，0）；
（2）当x=-$\frac{1}{2}$或$\frac{3}{2}$时，y=0；方程x2-x-$\frac{3}{4}$=0的解是x1=-$\frac{1}{2}$，x2=$\frac{3}{2}$；
（3）当x取-$\frac{1}{2}$＜x＜$\frac{3}{2}$时，y＜0；当x取x＜-$\frac{1}{2}$或x＞$\frac{3}{2}$时，y＞0；
（4）x2-x-$\frac{3}{4}$＜0的解集是-$\frac{1}{2}$＜x＜$\frac{3}{2}$，x2-x-$\frac{3}{4}$＞0的解集是x＜-$\frac{1}{2}$或x＞$\frac{3}{2}$．
故答案为：（1）（-$\frac{1}{2}$，0），（$\frac{3}{2}$，0）；（2）-$\frac{1}{2}$或$\frac{3}{2}$；x1=-$\frac{1}{2}$，x2=$\frac{3}{2}$；（3）-$\frac{1}{2}$＜x＜$\frac{3}{2}$；x＜-$\frac{1}{2}$或x＞$\frac{3}{2}$，（4）-$\frac{1}{2}$＜x＜$\frac{3}{2}$；x＜-$\frac{1}{2}$或x＞$\frac{3}{2}$．
点评 本题考查了二次函数与不等式组，抛物线与x轴的交点问题，数形结合是数学中的重要思想之一，解决函数问题更是如此，同学们要引起重视．
如图，△ABC的两条高AD、BF交于E，连EC，∠AEB=105°，∠ABC=45°．| A． | $\frac{12（x-y）}{15（x+y）}$ | B． | $\frac{{y}^{2}-{x}^{2}}{x+y}$ | ||
| C． | $\frac{{x}^{2}+{y}^{2}}{{x}^{2}y+x{y}^{2}}$ | D． | $\frac{{x}^{2}-{y}^{2}}{（x+y）^{2}}$ |