Question

【题目】已知：在平面直角坐标系中，抛物线与轴交于点、，与轴交于点，抛物线的顶点到轴的距离为，．

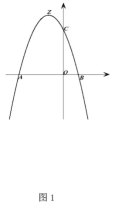
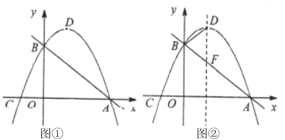
（1）如图1，求抛物线的解析式；

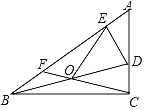
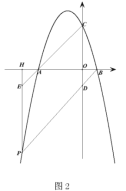
（2）如图2，点为第三象限内的抛物线上一点，连接交轴于点，过点作轴于点，连接并延长交于点，求证：；

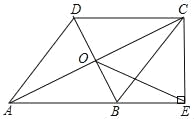
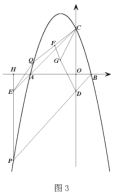
（3）如图3，在（2）的条件下，点为第二象限内的抛物线上的一点，分别连接、，点为的中点，点为第二象限内的一点，分别连接，，，且，，若，求点的横坐标．

Answer 1

【答案】（1）y=；（2）见详解；（3）

【解析】

（1）把化为函数的顶点式y=，得到顶点坐标Z（-1，4），即可得出m=4，令y=0，求出x的值，即为A、B两点的横坐标，根据即可求出a的值，代入函数解析式即可；

（2）由（1）可得出点A（-3，0），点B（1，0），点C（0，3），设P（t， ），利用PH∥y轴得出，推出OD=-t-3，进而证得EH=AH=-3-t即可得出结论；

（3）连接DE，延长CG交DE于N，可证得2∠QEH=∠ENQ，通过作CK⊥DQ，推出△CKD≌△EQD，设QK=x，利用勾股定理得到方程，解出x=，由等积法求出QM，进而得出tan∠QCM，设Q点坐标（m，-），由，解出m值即得到点Q的横坐标．

（1）根据题意知，，

=，

∴顶点Z的坐标为（-1，4），

∵顶点Z到x轴距离为4，

∴m=4，

令y=0，则，

解得x==，

∴A（，0），B（，0），

∵AB==，

∴=，

∴a=1，

∴抛物线的解析式为y=，

故答案为：y=；

（2）由（1）知，点A（-3，0），点B（1，0），点C（0，3），

设P（t， ），

∵PH⊥x轴，即PH∥y轴，

∴H（t，0），且，PH=，BH=1-t，OB=1，

∴，

∴OD===-t-3，

∵OA=3，OC=3，

∴∠CAO=∠HAE=45°，

∴EH=AH=-3-t，

∴OD=EH；

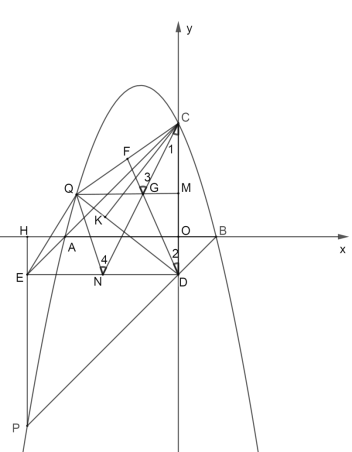
（3）连接DE，延长CG交DE于N，

∵EH=OD，EH∥OD，

∴DE∥x轴，

∴∠CDE=90°，

∵CG=DG，

∴G为CN中点，

∴FG∥QN，且FG=QN，

∵CD=4FG，

∴CD=2QN，

∵∠CDG=∠2=∠1，

∴90°+∠CDG=∠90°+∠1=∠CNE，

∴∠CNE-∠CGF=∠CNE-∠4，

∴2∠QEH=∠ENQ，

设∠QEH=，∠ENQ=2，

∴∠QEN=90°-=∠EQN，

∴QN=EN，

∵CD=ED，

∴DE=2EN，

∴ND=EN=QN，

∴∠EQD=90°，

过点C作CK⊥DQ，

M型全等，

∴△CKD≌△EQD，

∴EQ=DK，CK=QD，

设EQ=3=DK，

CQ=，

QK=x，

∴CK=x+3，

∴，

∴，

∴，（舍），

∴CK=+3=4，

∴CD=5，

等积法：

QD×CK=CD×QM，

∴4×4=5×QM，

QM=，

∴CM=，

∴tan∠QCM=，

设Q（m，-），

∴QM=-m，CM=3-（-）=，

∴，

∴16+45m=0，

∴（舍），，

∴，

故答案为：．