题目内容
已知：如图，梯形ABCD中，AB∥CD，中位线EF长为20，AC与EF交于点G，GF-GE=5．
求AB、CD的长．
解：在梯形ABCD中，AB∥CD，
∵中位线EF长为20，
∴GF+GE=20，
又∵GF-GE=5，
解得 GF=
，GE=
．
∵EF∥AB∥CD，
∴G为AC中点，
∴AB=2GF=25，
CD=2GE=15．
分析：根据三角形的中位线定理可得出EF=
（AB+CD），GF=AB，GE=CD，从而得出AB、CD的长．
点评：本题考查了梯形的中位线定理以及三角形的中位线定理，是基础知识要熟练掌握．
∵中位线EF长为20，
∴GF+GE=20，
又∵GF-GE=5，
解得 GF=
，GE=．∵EF∥AB∥CD，
∴G为AC中点，
∴AB=2GF=25，
CD=2GE=15．
分析：根据三角形的中位线定理可得出EF=
（AB+CD），GF=AB，GE=CD，从而得出AB、CD的长．点评：本题考查了梯形的中位线定理以及三角形的中位线定理，是基础知识要熟练掌握．
练习册系列答案
相关题目
9、已知：如图，梯形ABCD中，AD∥BC，AB=CD，对角线AC与BD相交于点O，则图中全等三角形共有（ ）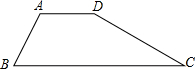
已知：如图，梯形ABCD中，AD∥BC，∠DAB=120°，tanC=
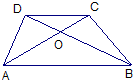8、已知，如图，梯形ABCD中，AB∥CD，△COD与△AOB的周长比为1：2，则CD：AB=
已知：如图，梯形ABCD中，AB∥CD，AD=BC，对角线AC、BD交于M，AB=2，CD=4，∠CMD=90°，求：BD的长．