题目内容
 已知:如图,梯形ABCD中,AB∥CD,AD=BC,对角线AC、BD交于M,AB=2,CD=4,∠CMD=90°,求:BD的长.
已知:如图,梯形ABCD中,AB∥CD,AD=BC,对角线AC、BD交于M,AB=2,CD=4,∠CMD=90°,求:BD的长.分析:过点B作BE∥AC交DC的延长线于点E,根据∠CMD=90°求出△BDE是直角三角形,结合AB∥CD可以证明四边形ACEB是平行四边形,根据平行四边形对边相等可得AC=BE,CE=AB,从而求出DE的长度,然后根据等腰梯形的对角线相等推出BD=BE,利用勾股定理列式计算即可求出BD的长.
解答: 解:如图,过点B作BE∥AC交DC的延长线于点E,
解:如图,过点B作BE∥AC交DC的延长线于点E,
∴∠EBD=∠CMD=90°,
∵AB∥CD,
∴四边形ACEB是平行四边形,
∴AC=BE,CE=AB,
∵AB=2,CD=4,
∴DE=DC+CE=DC+AB=4+2=6,
∵梯形ABCD中,AB∥CD,AD=BC,
∴AC=BD,
∴BD=BE,
在Rt△BDE中,由勾股定理得,BD2+BE2=DE2,
即BD2+BD2=62,
解得BD=3
.
故答案为:3
.
 解:如图,过点B作BE∥AC交DC的延长线于点E,
解:如图,过点B作BE∥AC交DC的延长线于点E,∴∠EBD=∠CMD=90°,
∵AB∥CD,
∴四边形ACEB是平行四边形,
∴AC=BE,CE=AB,
∵AB=2,CD=4,
∴DE=DC+CE=DC+AB=4+2=6,
∵梯形ABCD中,AB∥CD,AD=BC,
∴AC=BD,
∴BD=BE,
在Rt△BDE中,由勾股定理得,BD2+BE2=DE2,
即BD2+BD2=62,
解得BD=3
| 2 |
故答案为:3
| 2 |
点评:本题主要考查了等腰梯形的对角线相等的性质,平行四边形的判定与性质,勾股定理的应用,作出辅助线把对角线的垂直转化为直角三角形是解题的关键,也是解决等腰梯形问题常作的辅助线之一.

练习册系列答案
相关题目
 9、已知:如图,梯形ABCD中,AD∥BC,AB=CD,对角线AC与BD相交于点O,则图中全等三角形共有( )
9、已知:如图,梯形ABCD中,AD∥BC,AB=CD,对角线AC与BD相交于点O,则图中全等三角形共有( )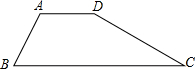 已知:如图,梯形ABCD中,AD∥BC,∠DAB=120°,tanC=
已知:如图,梯形ABCD中,AD∥BC,∠DAB=120°,tanC=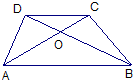 8、已知,如图,梯形ABCD中,AB∥CD,△COD与△AOB的周长比为1:2,则CD:AB=
8、已知,如图,梯形ABCD中,AB∥CD,△COD与△AOB的周长比为1:2,则CD:AB=