Question

【题目】如图，在Rt△ABC中，∠C=90°，CA=12 cm，BC=12cm；动点P从点C开始沿CA以2 cm/s的速度向点A移动，动点Q从点A开始沿AB以4cm/s的速度向点B移动，动点R从点B开始沿BC以 2cm/s的速度向点C移动．如果P、Q、R分别从C、A、B同时移动，移动时间为t（0＜t＜6）s．

（1）∠CAB的度数是；
（2）以CB为直径的⊙O与AB交于点M，当t为何值时，PM与⊙O相切？
（3）写出△PQR的面积S随动点移动时间t的函数关系式，并求S的最小值及相应的t值；
（4）是否存在△APQ为等腰三角形？若存在，求出相应的t值；若不存在请说明理由．

Answer 1

【答案】
（1）30°
（2）解：如图1，连接OP，OM．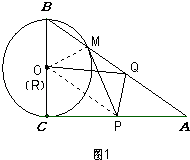

当PM与⊙O相切时，有∠PMO=∠PCO=90°，

∵MO=CO，PO=PO，

∴Rt△PMO≌Rt△PCO，

∴∠MOP=∠COP；

由（1）知∠OBA=60°，

∵OM=OB，

∴△OBM是等边三角形，

∴∠BOM=60°，

∴∠MOP=∠COP=60°，

∴CP=COtan∠COP=6tan60°=6 ，

又∵

∴2 t=6

∴t=3，

即：t=3s时，PM与⊙O相切；

（3）解：如图2，过点Q作QE⊥AC于点E，

∵∠BAC=30°，AQ=4t，

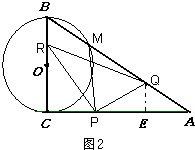
∴ AE=AQcos∠BAC=4tcos30°=2 t，

∴

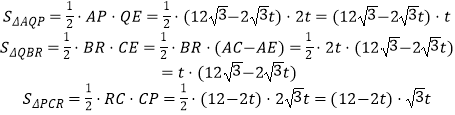
∴S△PQR=S△ACB﹣S△AQP﹣S△QBR﹣S△PCR

，

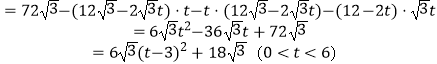∴当t=3s时， cm2；

（4）解：存在．如图3，

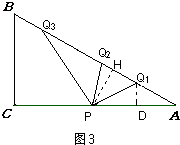
分三种情况：

①PQ1=AQ1=4t时，过点Q1作Q1D⊥AC于点D，

则 ，

∴ ，

∴t=2；

②当AP=AQ2=4t时，

∵ ，

∴ ，

③当PA=PQ3=4t时，

过点P作PH⊥AB于点H，

AH=PAcos30°= =18﹣3tAQ3=2AH=36﹣6t，

∴36﹣6t=4t，

∴t=3.6，

综上所述，当 s时，△APQ是等腰三角形．

【解析】解：（1）∵∠C=90°，CA=12 cm，BC=12cm，

∴tan∠CAB= ，

∴∠CAB=30°，

所以答案是：30°；

【考点精析】根据题目的已知条件，利用锐角三角函数的定义和特殊角的三角函数值的相关知识可以得到问题的答案，需要掌握锐角A的正弦、余弦、正切、余切都叫做∠A的锐角三角函数；分母口诀：30度、45度、60度的正弦值、余弦值的分母都是2，30度、45度、60度的正切值、余切值的分母都是3，分子口诀：“123，321，三九二十七”．