题目内容
设a= +
+ +
+ +…+
+…+ ,问与a最接近的整数是多少?
,问与a最接近的整数是多少?
解:∵n为任意的正整数,
∴ =
=
= =
= =1+
=1+ ,
,
∴a=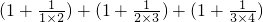 +…+(1+
+…+(1+ )
)
=2000+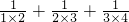 +…+
+…+
=2000+(1- )+(
)+( -
- )+(
)+( -
- )+…+
)+…+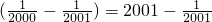 .
.
因此,与a最接近的整数是2001.
分析:通过上式找出规律,得出通项公式: 再进行化简,得结果为1+
再进行化简,得结果为1+ ,将自然数n代入求出结果,再判断与a最接近的整数.
,将自然数n代入求出结果,再判断与a最接近的整数.
点评:点拨:①化一般式为有理式,②用裂项法将分数 化成
化成 -
- ,然后求和.
,然后求和.
∴
 =
=
=
 =
= =1+
=1+ ,
,∴a=
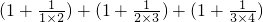 +…+(1+
+…+(1+ )
)=2000+
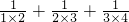 +…+
+…+
=2000+(1-
 )+(
)+( -
- )+(
)+( -
- )+…+
)+…+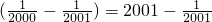 .
.因此,与a最接近的整数是2001.
分析:通过上式找出规律,得出通项公式:
 再进行化简,得结果为1+
再进行化简,得结果为1+ ,将自然数n代入求出结果,再判断与a最接近的整数.
,将自然数n代入求出结果,再判断与a最接近的整数.点评:点拨:①化一般式为有理式,②用裂项法将分数
 化成
化成 -
- ,然后求和.
,然后求和. 
练习册系列答案
相关题目
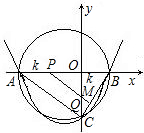 物线的解析式为y=
物线的解析式为y=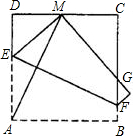 将正方形ABCD折叠,使顶点A与CD边上的点M重合,折痕交AD于E,交BC于F,边AB折叠后与BC边交于点G(如图).
将正方形ABCD折叠,使顶点A与CD边上的点M重合,折痕交AD于E,交BC于F,边AB折叠后与BC边交于点G(如图).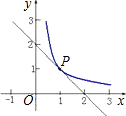 已知:如图所示,反比例函数y=
已知:如图所示,反比例函数y= (4,n).
(4,n). 如图,已知:∠MAN=30°,O为边AN上一点,以O为圆心,2为半径作⊙O,交AN于D,E两点,设AD=x,问:当x为何值时,⊙O与AM相切?
如图,已知:∠MAN=30°,O为边AN上一点,以O为圆心,2为半径作⊙O,交AN于D,E两点,设AD=x,问:当x为何值时,⊙O与AM相切?