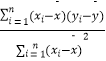题目内容
【题目】已知直线l的极坐标方程为ρsin(θ+ ![]() )=
)= ![]() ,圆C的参数方程为:
,圆C的参数方程为: ![]() (其中θ为参数).
(其中θ为参数).
(1)判断直线l与圆C的位置关系;
(2)若椭圆的参数方程为 ![]() (φ为参数),过圆C的圆心且与直线l垂直的直线l′与椭圆相交于A,B两点,求|AB|.
(φ为参数),过圆C的圆心且与直线l垂直的直线l′与椭圆相交于A,B两点,求|AB|.
【答案】
(1)解:将直线l的极坐标方程 ![]() ,化为直角坐标方程:x+y﹣1=0.
,化为直角坐标方程:x+y﹣1=0.
将圆C的参数方程化为普通方程:x2+(y+2)2=4,圆心为C(0,﹣2),半径r=2.
∴圆心C到直线l的距离为d= ![]() >r=2,
>r=2,
∴直线l与圆C相离.
(2)解:将椭圆的参数方程化为普通方程为 ![]() ,
,
∵直线l:x+y﹣1=0的斜率为k1=﹣1,
∴直线l'的斜率为k2=1,即倾斜角为 ![]() ,
,
则直线l'的参数方程为 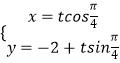 ,(t为参数),
,(t为参数),
即 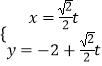 (t为参数),
(t为参数),
把直线l'的参数方程 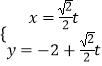 代入
代入 ![]() ,
,
整理得7t2﹣16 ![]() t+8=0.(*)
t+8=0.(*)
由于△=(﹣16 ![]() )2﹣4×7×8>0,
)2﹣4×7×8>0,
故可设t1,t2是方程(*)的两个不等实根,则有t1t2= ![]() ,
, ![]() ,
,
|AB|= ![]()
【解析】(1)将直线l的极坐标方程化为直角坐标方程,将圆C的参数方程化为普通方程,求出圆心C到直线l的距离,由此得到直线l与圆C相离.(2)将椭圆的参数方程化为普通方程为 ![]() ,求出直线l'的参数方程,把直线l'的参数方程代入椭圆的普通方程,得7t2﹣16
,求出直线l'的参数方程,把直线l'的参数方程代入椭圆的普通方程,得7t2﹣16 ![]() t+8=0,由此利用根的判别式、韦达定理、弦长公式能求出|AB|.
t+8=0,由此利用根的判别式、韦达定理、弦长公式能求出|AB|.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案
相关题目