题目内容
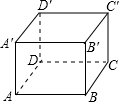
已知长方体的长为6cm，宽为5cm，高为3cm，那么一只虫子想从A爬到B最短路程是（ ）分析：根据题意画出符合条件的两种情况，根据勾股定理求出即可．
解答：解：
①如图1，连接AB，则AB是A、B之间的最短距离，
AC=6cm，BC=3cm+5cm=8cm，∠C=90°，由勾股定理得：AB=10cm；
②如图2，AC=6cm+5cm=11cm，BC=3cm，∠C=90°，由勾股定理得：AB=
cm；
∵10＜
，
∴选B．
①如图1，连接AB，则AB是A、B之间的最短距离，
AC=6cm，BC=3cm+5cm=8cm，∠C=90°，由勾股定理得：AB=10cm；
②如图2，AC=6cm+5cm=11cm，BC=3cm，∠C=90°，由勾股定理得：AB=
| 130 |
∵10＜
| 130 |
∴选B．
点评：本题考查了勾股定理和两点之间的距离的应用，关键是能知道求那一条线段的长．
练习册系列答案
名校课堂系列答案
相关题目
如图，地面上有一个长方体，一只蜘蛛在这个长方体的顶点A处，一滴水珠在这个长方形的顶点C′处，已知长方体的长为6m，宽为5m，高为3m，蜘蛛要沿着长方体的表面从A处爬到C′处，则蜘蛛爬行的最短距离为（ ）
如图，地面上有一个长方体，一只蜘蛛在这个长方体的顶点A处，一滴水珠在这个长方形的顶点C′处，已知长方体的长为6m，宽为5m，高为3m，蜘蛛要沿着长方体的表面从A处爬到C′处，则蜘蛛爬行的最短距离为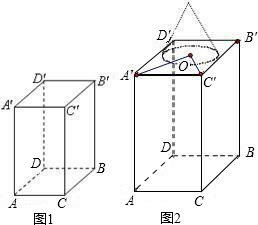
如图1，已知长方体的长为BC=2cm，宽AC=1cm，高AA′=4cm．
已知长方体的长为6cm，宽为5cm，高为3cm，那么一只虫子想从A爬到B最短路程是
cm