题目内容
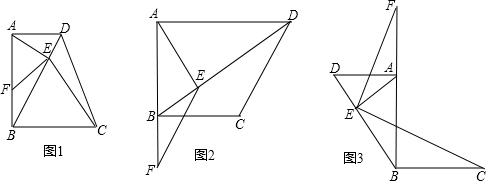
如图(1),在△ABC中,AE平分∠BAC(∠C>∠B),F为AE上一点,且FD⊥BC于D.(1)试推导∠EFD与∠B、∠C的大小关系;
(2)如图(2),当点F在AE的延长线上时,其余条件都不变,判断你在(1)中推导的结论是否还成立?
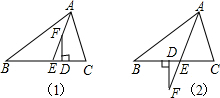
分析:先根据AE平分∠BAC推出∠BAE=
∠BAC=
[180°-(∠B+∠C)],再根据外角的定义求出∠FED=∠B+∠BAE,然后利用直角三角形的性质求出∠EFD=90°-∠FED.
| 1 |
| 2 |
| 1 |
| 2 |
解答: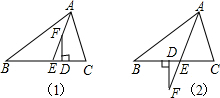 解:(1)∵AE平分∠BAC,
解:(1)∵AE平分∠BAC,
∴∠BAE=
∠BAC.
∵∠BAC=180°-(∠B+∠C);
∴∠BAE=
[180°-(∠B+∠C)];
∴∠FED=∠B+∠BAE=∠B+
[180°-(∠B+∠C)]=90°+
(∠B-∠C).
又∵FD⊥BC,
∴∠FDE=90°;
∴∠EFD=90°-[90°+
(∠B-∠C)]=
(∠C-∠B).
(2)∵AE平分∠BAC,
∴∠BAE=
∠BAC.
∵∠BAC=180°-(∠B+∠C);
∴∠BAE=
[180°-(∠B+∠C)];
∴∠FED=∠B+∠BAE=∠B+
[180°-(∠B+∠C)]=90°+
(∠B-∠C).
又∵FD⊥BC,
∴∠FDE=90°;
∴∠EFD=90°-[90°+
(∠B-∠C)=
(∠C-∠B)].
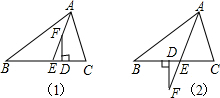 解:(1)∵AE平分∠BAC,
解:(1)∵AE平分∠BAC,∴∠BAE=
| 1 |
| 2 |
∵∠BAC=180°-(∠B+∠C);
∴∠BAE=
| 1 |
| 2 |
∴∠FED=∠B+∠BAE=∠B+
| 1 |
| 2 |
| 1 |
| 2 |
又∵FD⊥BC,
∴∠FDE=90°;
∴∠EFD=90°-[90°+
| 1 |
| 2 |
| 1 |
| 2 |
(2)∵AE平分∠BAC,
∴∠BAE=
| 1 |
| 2 |
∵∠BAC=180°-(∠B+∠C);
∴∠BAE=
| 1 |
| 2 |
∴∠FED=∠B+∠BAE=∠B+
| 1 |
| 2 |
| 1 |
| 2 |
又∵FD⊥BC,
∴∠FDE=90°;
∴∠EFD=90°-[90°+
| 1 |
| 2 |
| 1 |
| 2 |
点评:此题主要考查了角平分线的性质、三角形内角和定理和直角三角形的性质,命题时经常将多个知识点联系在一起进行考查,这样更能训练学生的解题能力.

练习册系列答案
相关题目
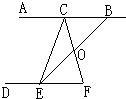 28、如图,C、E分别在AB、DF上,小华想知道∠ACE和∠DEC是否互补,但是他有没有带量角器,只带了一副三角尺,于是他想了这样一个办法:首先连接CF,再找出CF的中点O,然后连接EO并延长EO和直线AB相交于点B,经过测量,他发现EO=BO,因此他得出结论:∠ACE和∠DEC互补,而且他还发现BC=EF.以下是他的想法,请你填上根据.
28、如图,C、E分别在AB、DF上,小华想知道∠ACE和∠DEC是否互补,但是他有没有带量角器,只带了一副三角尺,于是他想了这样一个办法:首先连接CF,再找出CF的中点O,然后连接EO并延长EO和直线AB相交于点B,经过测量,他发现EO=BO,因此他得出结论:∠ACE和∠DEC互补,而且他还发现BC=EF.以下是他的想法,请你填上根据.