Question

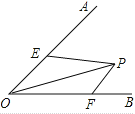
【题目】已知∠AOB的大小为α，P是∠AOB内部的一个定点，且OP＝2，点E、F分别是OA、OB上的动点，若△PEF周长的最小值等于2，则α＝（ ）

A. 30° B. 45° C. 60° D. 90°

Answer 1

【答案】A

【解析】如图,作点P关于OA的对称点C,关于OB的对称点D,连接CD,交OA于E,OB于F,此时, △PEF的周长最小,连接OC,OD,PE,PF,

因为点P与点C关于OA对称,所以OA垂直平分PC,所以∠COA=∠AOP,PE=CE,OC=OP,

同理可得, ∠DOB=∠BOP,PF=DF,OD=OP,

所以∠COA+∠DOB=∠AOP+∠BOP=∠AOB=a,OC=OD=OP=2,

所以∠COD=2a,

又因为△PEF的周长=PE+EF+FP=CE+EF+FD=CD=2,

所以OC=OD=CD=2,

所以△COD是等边三角形,

所以2a=60°,

所以a=30°,

故选A.