题目内容
【题目】二次函数![]() (
(![]() 是常数,
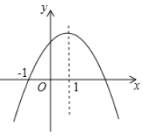
是常数,![]() )的图象如图所示,下列结论:①
)的图象如图所示,下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;⑤
;⑤![]() ,其中错误的结论有( )个.
,其中错误的结论有( )个.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】B
【解析】
根据图象的开口方向可确定a,结合对称轴可确定b,根据图象与y轴的交点位置可确定c,根据图象与x轴的交点个数可确定![]() ,根据当x=-2时,y<0,抛物线与x轴的另一个交点的交点的坐标是(3,0),即可得出结论.
,根据当x=-2时,y<0,抛物线与x轴的另一个交点的交点的坐标是(3,0),即可得出结论.
解:∵开口方向向下
∴a<0
∵图象与y轴交于正半轴
∴c>0
∵对称轴在y轴右侧
∴b>0
∴abc<0,故①正确;
∵二次函数的对称轴是直线x=1,即二次函数的顶点的横坐标为![]() =1
=1
∴2a+b=0,故②错误;
∵抛物线与x轴有两个交点
∴b2-4ac>0,即b2>4ac,故③错误;
∵![]()
∴b=-2a
∴可将抛物线的解析式化为y=ax2-2ax+c(a≠0)
由图象可知:当x=-2时,y<0
即4a-(-4a)+c=8a+c<0,故④正确;
∵二次函数的图象与x轴的一个交点是(-1,0),对称轴是直线x=1
∴另一个交点的坐标是(3,0)
∴设![]()
即a=a,b=-2a,c=-3a
∴a∶b∶c=a∶(-2a)∶(-3a)=-1∶2∶3,故⑤正确.
故选B.

练习册系列答案
相关题目
【题目】公司以10元/千克的价格收购一批产品进行销售,经过市场调查获悉,日销售量y(千克)是销售价格x(元/千克)的一次函数,部分数据如表:
销售价格x(元/千克) | 10 | 15 | 20 | 25 | 30 |
日销售量y(千克) | 300 | 225 | 150 | 75 | 0 |
(1)直接写出y与x之间的函数表达式;
(2)求日销售利润为150元时的销售价格;
(3)若公司每销售1千克产品需另行支出a元(0<a<10)的费用,当20≤x≤25时,公司的日获利润的最大值为1215元,求a的值.