��Ŀ����
����Ŀ������������ѧ��������Ҫ�о��������Ǿ����������ν�ϡ�����ת���ķ������һЩ��ѧ���⣮����������̽��������˼�Σ������������ķ����ڽ�����������е�Ӧ�ã�
��1��̽��![]() �ļ������壺��ͼ�٣���ֱ������ϵ�У����M������Ϊ(x��y)����M��MP��x����P����MQ��y����Q����P������Ϊ(x��0)��Q������Ϊ(0��y)����OP��|x|��OQ��|y|���ڡ�OPM�У�PM��OQ��|y|����MO��
�ļ������壺��ͼ�٣���ֱ������ϵ�У����M������Ϊ(x��y)����M��MP��x����P����MQ��y����Q����P������Ϊ(x��0)��Q������Ϊ(0��y)����OP��|x|��OQ��|y|���ڡ�OPM�У�PM��OQ��|y|����MO��![]() ����ˣ�
����ˣ�![]() �ļ��������������Ϊ��M(x��y)���O(0��0)֮��ľ���OM��
�ļ��������������Ϊ��M(x��y)���O(0��0)֮��ľ���OM��
��![]() �ļ��������������Ϊ��N1�� ������д���꣩���O(0��0)֮��ľ���N1O��
�ļ��������������Ϊ��N1�� ������д���꣩���O(0��0)֮��ľ���N1O��
�ڵ�N2(5����1)���O(0��0)֮��ľ���ON2Ϊ�� ����
��2��̽��![]() �ļ������壺��ͼ�ڣ���ֱ������ϵ�У����A�������Ϊ��x��1��y��5������̽����1����֪��A��O��
�ļ������壺��ͼ�ڣ���ֱ������ϵ�У����A�������Ϊ��x��1��y��5������̽����1����֪��A��O��![]() �����߶�A��O������ƽ��1����λ��������ƽ��5����λ���õ��߶�AB����ʱ��A������Ϊ��x��y������B������Ϊ��1��5������ΪAB��A��O������AB��
�����߶�A��O������ƽ��1����λ��������ƽ��5����λ���õ��߶�AB����ʱ��A������Ϊ��x��y������B������Ϊ��1��5������ΪAB��A��O������AB��![]() �����
�����![]() �ļ��������������Ϊ��A��x��y�����B��1��5��֮��ľ��룮
�ļ��������������Ϊ��A��x��y�����B��1��5��֮��ľ��룮
��3��̽��![]() �ļ������壺�����̽������2���ķ�������ͼ���л���ͼ�Σ���ô
�ļ������壺�����̽������2���ķ�������ͼ���л���ͼ�Σ���ô![]() �ļ��������������Ϊ��C�� ������д���꣩���D(x��y)֮��ľ��룮
�ļ��������������Ϊ��C�� ������д���꣩���D(x��y)֮��ľ��룮
��4����չӦ�ã���![]()
![]() �ļ��������������Ϊ����A(x��y)���E(1����4)�ľ������A(x��y)���F�� ������д���꣩�ľ���֮�ͣ�
�ļ��������������Ϊ����A(x��y)���E(1����4)�ľ������A(x��y)���F�� ������д���꣩�ľ���֮�ͣ�
��![]() ����СֵΪ�� ����ֱ��д�������
����СֵΪ�� ����ֱ��д�������
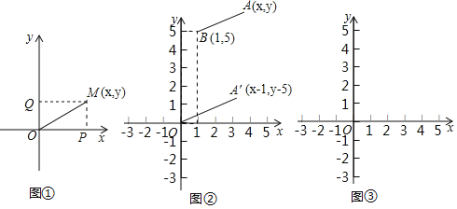
���𰸡���1����(��2��3)��(3����2)����![]() ����3���������� (��2��3)����4����(��2����3)����
����3���������� (��2��3)����4����(��2����3)����![]()
��������
(1)�ٹ���ֱ�����������ù��ɶ������ɵó��𰸣�
���������ľ��뼴�ɵó��𰸣�
(3)���D��������Ϊ![]() ���������ľ����ƽ�Ƶ����ʼ��ɵó����ۣ�
���������ľ����ƽ�Ƶ����ʼ��ɵó����ۣ�
(4)����(3)���ɵó��𰸣�
�ڸ��������ε����߹�ϵ��������𰸣�
(1)��![]() �ļ��������������Ϊ��N1
�ļ��������������Ϊ��N1 ![]() ��
��![]() ���O
���O![]() ֮��ľ���N1O��
֮��ľ���N1O��
�ʴ�Ϊ��![]() ��
��![]() ��
��
�ڵ�N2![]() ���O
���O![]() ֮��ľ���ON2Ϊ��
֮��ľ���ON2Ϊ��![]() ��
��
�ʴ�Ϊ��![]() ��
��
(3)���D��������Ϊ![]() ����ͼ����ʾ��
����ͼ����ʾ��
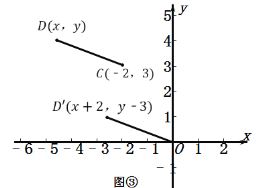
��̽��(2)��֪��D��O=![]() ��
��
���߶�D��O������ƽ��2����λ��������ƽ��3����λ���õ��߶�CD��
��ʱ��D������Ϊ![]() ����C������Ϊ
����C������Ϊ![]() ��
��
��CD=D'O��
��CD=![]() ��
��
��![]() �ļ�������Ϊ��C
�ļ�������Ϊ��C![]() ����D
����D![]() ֮��ľ��룻
֮��ľ��룻
�ʴ�Ϊ��![]() ��
��
(4)����(2)��֪�� ![]()
![]() �ļ��������������Ϊ��
�ļ��������������Ϊ��
��A![]() ���E
���E![]() �ľ������A
�ľ������A![]() ���F
���F![]() �ľ���֮�ͣ�
�ľ���֮�ͣ�
�ʴ�Ϊ��![]() ��
��
�ڵ�A![]() λ��ֱ��EF��ʱ��
λ��ֱ��EF��ʱ��
��ʱ��A��E��F������ɡ�AEF��
�������������߹�ϵ��֪��EF��AF+AE��
����Aλ���߶�EF֮��ʱ����ʱEF=AF+AE��
��![]() ����СֵΪEF�ľ��룬
����СֵΪEF�ľ��룬
��EF=![]() ��
��
�ʴ�Ϊ��![]() ��
��