题目内容
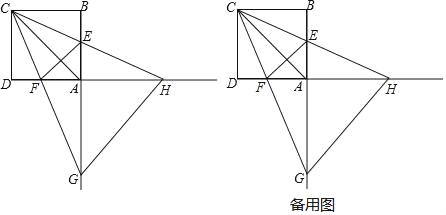
【题目】如图是云梯升降车示意图,其点A位置固定,AC可伸缩且可绕点A转动,已知点A距离地面BD的高度AH为3.4米.当AC长度为9米,张角∠HAC为119°时,求云梯升降车最高点C距离地面的高度.(结果保留一位小数)参考数据:sin29°≈0.49,cos29°≈0.88,tan29°≈0.55

【答案】云梯升降车最高点C距离地面的高度为7.8m.
【解析】
作CE⊥BD于E,AF⊥CE于F,如图,易得四边形AHEF为矩形,则EF=AH=3.4m,∠HAF=90°,再计算出∠CAF=29°,则在Rt△ACF中利用正弦可计算出CF,然后计算CF+EF即可.
作CE⊥BD于E,AF⊥CE于F,如图,
易得四边形AHEF为矩形,
∴EF=AH=3.4m,∠HAF=90°,
∴∠CAF=∠CAH-∠HAF=119°-90°=29°,
在Rt△ACF中,∵sin∠CAF=![]() ,
,
∴CF=9sin29°=9×0.49=4.41,
∴CE=CF+EF=4.41+3.4≈7.8(m),
答:云梯升降车最高点C距离地面的高度为7.8m.


练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目