题目内容
如图:等圆⊙O1和⊙O2相交于A、B两点,⊙O1经过⊙O2的圆心,顺次连接A、O1、B、O2.
(1)求证:四边形AO1BO2是菱形;
(2)过直径AC的端点C作⊙O1的切线CE交AB的延长线于E,连接CO2交AE于D,求证:CE=2DO2;
(3)在(2)的条件下,若![]() ,求
,求![]() 的值.
的值.
 |
证明:(1)∵⊙O1与⊙O2是等圆,
∴![]() ······· 1分
······· 1分
∴四边形![]() 是菱形. ······· 2分
是菱形. ······· 2分
(2)∵四边形![]() 是菱形
是菱形
∴∠![]() =∠
=∠![]() ·········· 3分
·········· 3分
∵CE是⊙O1的切线,AC是⊙O1的直径,
∴∠![]() =∠
=∠![]() =90°
=90°
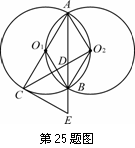 ∴△ACE∽△AO2D
∴△ACE∽△AO2D
![]() 即
即![]()
(3)∵四边形![]() 是菱形
是菱形
∴![]() ∥
∥![]() ∴△ACD∽△
∴△ACD∽△![]() ,
,
∴![]() ∴
∴![]() ,
,
∵![]() ∴
∴![]()

练习册系列答案
相关题目
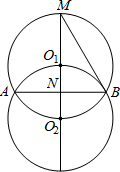 于点N,连接BM,已知AB=2
于点N,连接BM,已知AB=2
 (2012•桂林)如图,等圆⊙O1和⊙O2相交于A、B两点,⊙O1经过⊙O2的圆心,顺次连接A、O1、B、O2.
(2012•桂林)如图,等圆⊙O1和⊙O2相交于A、B两点,⊙O1经过⊙O2的圆心,顺次连接A、O1、B、O2.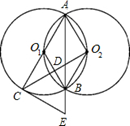
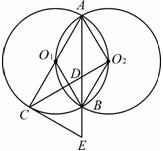
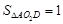 ,求
,求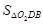 的值.
的值.