题目内容
如图，等圆⊙O1和⊙O2相交于A，B两点，⊙O2经过⊙O1的圆心O1，两圆的连心线交⊙O1于点M，交AB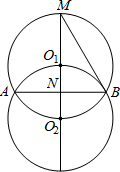
于点N，连接BM，已知AB=2| 3 |
（1）求证：BM是⊙O2的切线；
（2）求
 |
| AM |
分析：（1）连接O2B，由MO2是⊙O1的直径，得出∠MBO2=90°从而得出结论：BM是⊙O2的切线；
（2）根据O1B=O2B=O1O2，则∠O1O2B=60°，再由已知得出BN与O2B，从而计算出弧AM的长度．
（2）根据O1B=O2B=O1O2，则∠O1O2B=60°，再由已知得出BN与O2B，从而计算出弧AM的长度．
解答：
（1）证明：连接O2B，
∵MO2是⊙O1的直径，
∴∠MBO2=90°，
∴BM是⊙O2的切线；
（2）解：∵O1B=O2B=O1O2，
∴∠O1O2B=60°，
∵AB=2
，
∴BN=
，
∴O2B=2，
∴
=
=
=
．
（1）证明：连接O2B，∵MO2是⊙O1的直径，
∴∠MBO2=90°，
∴BM是⊙O2的切线；
（2）解：∵O1B=O2B=O1O2，
∴∠O1O2B=60°，
∵AB=2
| 3 |
∴BN=
| 3 |
∴O2B=2，
∴
|
| AM |
|
| BM |
| 120π×2 |
| 180 |
| 4π |
| 3 |
点评：本题考查了切线的判定和性质、弧长的计算以及相交两圆的性质，是基础知识要熟练掌握．
练习册系列答案
相关题目
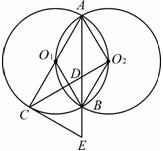
（2012•桂林）如图，等圆⊙O1和⊙O2相交于A、B两点，⊙O1经过⊙O2的圆心，顺次连接A、O1、B、O2．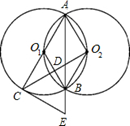
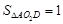，求
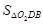的值．