题目内容
 探索与应用
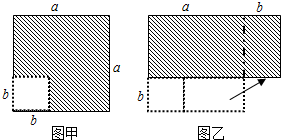
探索与应用【列式】在边长为a的正方形中挖去一个边长为b的小正方形(a>b)(如图甲),把余下的部分剪拼成一个长方形(如图乙),试用a、b列式:
图甲中阴影部分的面积为
a2-b2
a2-b2
,图乙中阴影部分的面积为(a+b)(a-b)
(a+b)(a-b)
.【填表】根据表格所给的a、b的值,计算a2-b2与(a+b)(a-b)的值,并将计算结果填入表中
| a | 2 | 0 | -2 | … | ||||
| b | -3 |
|
1 | … | ||||
| a2-b2 | -5 -5 |
-
-
|
3 3 |
… | ||||
| (a+b)(a-b) | -5 -5 |
-
-
|
3 3 |
… |
=
=
(a+b)(a-b)(填“>”,“=”或“<”)【应用】请你用你发现的结论进行简便运算:43.7452-56.2552.
分析:根据所给的图形用大正方形的面积减去小正方形的面积得出图甲中阴影部分的面积,再根据大正方形的边长减去b,再与大正方形的边长加上b进行相乘,即可求出图乙中阴影部分的面积;
填表时把a,b的值代入a2-b2和(a+b)(a-b)分别进行计算即可;
根据以上得出的结果可得a2-b2=(a+b)(a-b),在43.7452-56.2552进行计算时,利用得出的公式直接代入即可求出答案.
填表时把a,b的值代入a2-b2和(a+b)(a-b)分别进行计算即可;
根据以上得出的结果可得a2-b2=(a+b)(a-b),在43.7452-56.2552进行计算时,利用得出的公式直接代入即可求出答案.
解答:解:图甲中阴影部分的面积为:a2-b2,
图乙中阴影部分的面积为(a+b)(a-b);
∵a=2,b=-3,
∴a2-b2=22-(-3)2=4-9=-5,
∴(a+b)(a-b)=(2-3)(2+3)=-5;
∵a=0,b=
,
∴a2-b2=02-
2=0-
=-
,
∴(a+b)(a-b)=(0-
)(0+
)=-
;
∵a=-2,b=1,
∴a2-b2=(-2)2-12=4-1=3,
∴(a+b)(a-b)=(-2-1)(-2+1)=3;
填表如下:
根据以上得出的结果可得:a2-b2=(a+b)(a-b);
应用:
43.7452-56.2552=(43.745+56.255)(43.745-56.255)=100×(-12.51)=-1251.
故答案为:a2-b2,(a+b)(a-b),-5,-5,-
,-
,3,3,=.
图乙中阴影部分的面积为(a+b)(a-b);
∵a=2,b=-3,
∴a2-b2=22-(-3)2=4-9=-5,
∴(a+b)(a-b)=(2-3)(2+3)=-5;
∵a=0,b=
| 1 |
| 2 |
∴a2-b2=02-
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
∴(a+b)(a-b)=(0-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
∵a=-2,b=1,
∴a2-b2=(-2)2-12=4-1=3,
∴(a+b)(a-b)=(-2-1)(-2+1)=3;
填表如下:
| a | 2 | 0 | -2 | … | ||
| b | -3 |
|
1 | … | ||
| a2-b2 | -5 | -
|
3 | … | ||
| (a+b)(a-b) | -5 | -
|
3 | … |
应用:
43.7452-56.2552=(43.745+56.255)(43.745-56.255)=100×(-12.51)=-1251.
故答案为:a2-b2,(a+b)(a-b),-5,-5,-
| 1 |
| 4 |
| 1 |
| 4 |
点评:此题考查了平方差公式的应用,解题的关键是通过所给的图形证出a2-b2=(a+b)(a-b),再利用公式进行计算,是一道基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
探索与应用
【列 式】
在边长为 的正方形中挖去一个边长为
的正方形中挖去一个边长为 的小正方形(
的小正方形( >
> )(如图甲),把余下的部分剪拼成一个长方形(如图乙),
)(如图甲),把余下的部分剪拼成一个长方形(如图乙),
试用 、
、 列式:
列式:
图甲中阴影部分的面积为 ,
图乙中阴影部分的面积为 。
【填 表】
根据表格所给的a、b的值,计算 与
与 的值,并将计算结果填入表中
的值,并将计算结果填入表中
| a | 2 | 0 | -2 | … |
| b | -3 | 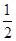 | 1 | … |
 | | | | … |
 | | | | … |
结合(1)、(2)中获得的经验,你能得出结论 :

 (填“>”,“=”或“<”)
(填“>”,“=”或“<”)【应 用】
请你用你发现的结论进行简便运算:

探索与应用
【列 式】
在边长为 的正方形中挖去一个边长为
的正方形中挖去一个边长为 的小正方形(
的小正方形( >
> )(如图甲),把余下的部分剪拼成一个长方形(如图乙),
)(如图甲),把余下的部分剪拼成一个长方形(如图乙),

试用 、
、 列式:
列式:
图甲中阴影部分的面积为 ,
图乙中阴影部分的面积为 。
【填 表】
根据表格所给的a、b的值,计算 与
与 的值,并将计算结果填入表中
的值,并将计算结果填入表中
|
a |
2 |
0 |
-2 |
… |
|
b |
-3 |
|
1 |
… |
|
|
|
|
|
… |
|
|
|
|
|
… |
【猜 想】
结合(1)、(2)中获得的经验,你能得出结论 :

 (填“>”,“=”或“<”)
(填“>”,“=”或“<”)
【应 用】
请你用你发现的结论进行简便运算:
 探索与应用
探索与应用
【列式】在边长为a的正方形中挖去一个边长为b的小正方形(a>b)(如图甲),把余下的部分剪拼成一个长方形(如图乙),试用a、b列式:
图甲中阴影部分的面积为______,图乙中阴影部分的面积为______.
【填表】根据表格所给的a、b的值,计算a2-b2与(a+b)(a-b)的值,并将计算结果填入表中
| a | 2 | 0 | -2 | … |
| b | -3 |  | 1 | … |
| a2-b2 | ______ | ______ | ______ | … |
| (a+b)(a-b) | ______ | ______ | ______ | … |
【应用】请你用你发现的结论进行简便运算:43.7452-56.2552.
