题目内容
【题目】如图,已知一条东西走向的河流,在河流对岸有一点A,小明在岸边点B处测得点A在点B的北偏东30°方向上,小明沿河岸向东走80m后到达点C,测得点A在点C的北偏西60°方向上,则点A到河岸BC的距离为 . 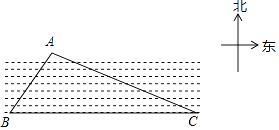
【答案】20 ![]() 米
米
【解析】方法1、过点A作AD⊥BC于点D.
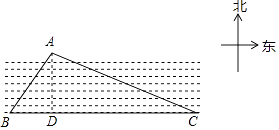
根据题意,∠ABC=90°﹣30°=60°,∠ACD=30°,
设AD=x米,
在Rt△ACD中,tan∠ACD= ![]() ,
,
∴CD= ![]() =
= ![]() =
= ![]() x,
x,
在Rt△ABD中,tan∠ABC= ![]() ,
,
∴BD= ![]() =
= ![]() =
= ![]() x,
x,
∴BC=CD+BD= ![]() x+
x+ ![]() x=80
x=80
∴x=20 ![]()
答:该河段的宽度为20 ![]() 米.
米.
故答案是:20 ![]() 米.
米.
方法2、过点A作AD⊥BC于点D.
根据题意,∠ABC=90°﹣30°=60°,∠ACD=30°,
∴∠BAC=180°﹣∠ABC﹣∠ACB=90°,
在Rt△ABC中,BC=80m,∠ACB=30°,
∴AB=40m,AC=40 ![]() m,
m,
∴S△ABC= ![]() AB×AC=
AB×AC= ![]() ×40×40
×40×40 ![]() =800
=800 ![]() ,
,
∵S△ABC= ![]() BC×AD=
BC×AD= ![]() ×80×AD=40AD=800
×80×AD=40AD=800 ![]() ,
,
∴AD=20 ![]() 米
米
答:该河段的宽度为20 ![]() 米.
米.
故答案是:20 ![]() 米.
米.
【考点精析】根据题目的已知条件,利用三角形的面积和锐角三角函数的定义的相关知识可以得到问题的答案,需要掌握三角形的面积=1/2×底×高;锐角A的正弦、余弦、正切、余切都叫做∠A的锐角三角函数.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目