题目内容
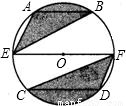
如图，⊙O的直径EF为10cm，弦AB、CD分别为6cm、8cm，且AB∥EF∥CD．则图中阴影部分面积之和为分析：由已知条件得出BM=3cm，DN=4cm，运用三角函数关系进而求出：∠MOB与∠DON的度数，再借助扇形的面积公式，求出阴影部分的面积．
解答：
解：作OM⊥AB，垂足为M，作ON⊥CD，垂足为N，
∵⊙O的直径EF为10cm，弦AB、CD分别为6cm、8cm，
且AB∥EF∥CD．
∴OA=OB=OC=OD=5cm，
BM=3cm，DN=4cm，
∵△AOB与△AEB等底同高，∴面积相等，
∴同理△OCD的面积等于△FCD的面积；
tan∠MOB=
，解得：∠MOB=36.87°，
∴∠AOB=73.74°
∵tan∠DON=
=
，∴∠DON=53.15°，∠COD=106.3°，
∴图中阴影部分面积之和为：
=
=
．
故答案为：
．
解：作OM⊥AB，垂足为M，作ON⊥CD，垂足为N，∵⊙O的直径EF为10cm，弦AB、CD分别为6cm、8cm，
且AB∥EF∥CD．
∴OA=OB=OC=OD=5cm，
BM=3cm，DN=4cm，
∵△AOB与△AEB等底同高，∴面积相等，
∴同理△OCD的面积等于△FCD的面积；
tan∠MOB=
| 3 |
| 4 |
∴∠AOB=73.74°
∵tan∠DON=
| DN |
| OD |
| 4 |
| 3 |
∴图中阴影部分面积之和为：
| nπr2 |
| 360 |
| 180π×25 |
| 360 |
| 25π |
| 2 |
故答案为：
| 25π |
| 2 |
点评：此题主要考查了扇形的面积求法，得出△OCD的面积等于△FCD的面积，与△AOB与△AEB等底同高面积相等，是解决问题的关键．
练习册系列答案
相关题目
10、如图，半圆的直径EF=10，正方形ABCD的顶点A、D在半圆上，一边BC在EF上，则这个正方形的面积等于
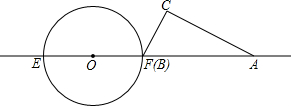
如图，⊙O的直径EF为5，弦AB、CD的长度分别为3和4，AB∥EF∥CD，则图中阴影部分的面积为