Question

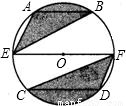
如图，⊙O的直径EF为5，弦AB、CD的长度分别为3和4，AB∥EF∥CD，则图中阴影部分的面积为

25π

8

．

Answer 1

分析：作直径MN，使MN⊥EF于O，交AB于G，交CD于H；连接OA、OB、OC、OD，将阴影部分的面积转化为扇形AOB和扇形COD的面积之和，然后确定∠AOB+∠COD的度数，继而可得出答案．

解答：解：作直径MN，使MN⊥EF于O，交AB于G，交CD于H；连接OA、OB、OC、OD，如图所示，
∵⊙O的直径EF为5，弦AB、CD分别为3、4，且AB∥EF∥CD．
∴OA=OB=OC=OD=2.5，BG=1.5，DH=2，
∵△AOB与△AEB等底同高，
∴S_△AOB=S_△AEB，
同理：S_△OCD=S_△FCD；
∴S_阴影=S_扇形OAB+S_扇形OCD，
在Rt△OBG中，BG=1.5，OB=2.5，
∴OG=

OB2-BG2

=2，
在Rt△OCH中，CH=2，OC=2.5，
∴OH=

OC2-CH2

=1.5，
sin∠DOF=sin∠ODH=

OH

OD

=

3

5

，sin∠BOG=

BG

OB

=

3

5

，
∴∠DOF=∠BOG，
∴∠BOG+∠DOH=90°，
同理可得：∠AOM+∠COH=90°，
S_阴影=S_扇形OAB+S_扇形OCD=

∠AOBπ×2.52

360

+

∠CODπ×2．52

360

=

180π×2．52

360

=

25π

8

．
故答案为：

25π

8

．

点评：本题考查了扇形面积的计算及垂径定理的知识，找出两个阴影部分面积之间的联系是解题的关键，有一定难度．