题目内容
如图,在△ABC中,∠C=90°,分别以A、B为圆心,以相等长度(大于 AB的长度)为半径画弧,得到两个交点M、N,作直线MN分别交AC、AB于E、D两点,连接EB,若∠EBC=28°,求∠A的度数.
AB的长度)为半径画弧,得到两个交点M、N,作直线MN分别交AC、AB于E、D两点,连接EB,若∠EBC=28°,求∠A的度数.
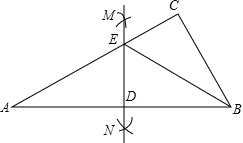
【考点】线段垂直平分线的性质.
【分析】根据直角三角形两锐角互余可得∠A+∠CBA=90°,由作图可得MN是AB的垂直平分线,由线段垂直平分线的性质可得AE=EB,再根据等边对等角可得∠A=∠EBA,然后再由∠EBC=28°可计算出∠A的度数.
【解答】解:∵∠C=90°,
∴∠A+∠CBA=90°,
由作图可得MN是AB的垂直平分线,
∴AE=EB,
∴∠A=∠EBA,
∵∠EBC=28°,
∴∠A= (90°﹣28°)=31°.
(90°﹣28°)=31°.
【点评】此题主要考查了线段垂直平分线的性质,以及三角形内角和定理,关键是掌握线段垂直平分线的作法.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

 的相反数是( )
的相反数是( )

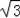
 ,1) B.(
,1) B.(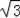
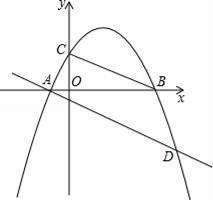


 的图象上一点,过点A作AB⊥y轴于点B,点P是x轴上的一个动点,则△ABP的面积为 .
的图象上一点,过点A作AB⊥y轴于点B,点P是x轴上的一个动点,则△ABP的面积为 .
