题目内容
 计算:
计算:
①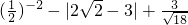 ;
;
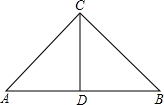
②如图,△ABC中,∠ACB=90°,AB= ,BC=2,求斜边AB上的高CD.
,BC=2,求斜边AB上的高CD.
③已知: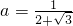 ,求
,求 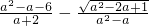 的值.
的值.
解:①原式=4-3+2 +
+ =1+
=1+ ;
;
②在Rt△ABC中,AB= ,BC=2,
,BC=2,
根据勾股定理得:AC= =2,
=2,
∵CD⊥AB,
∴S△ABC= AC•BC=
AC•BC= AB•CD,
AB•CD,
∴CD= =
=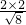 =
= ;
;
③∵a= =
=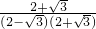 =2+
=2+ ,即a-1=2+
,即a-1=2+ -1=1+
-1=1+ >0,
>0,
原式=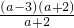 -
-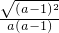 =a-3-
=a-3- =a-3-
=a-3- =2+
=2+ -3-2-
-3-2- =1.
=1.
分析:①原式第一项利用负指数公式化简,第二项先判断正负,再利用绝对值的代数意义化简,最后一项化为最简二次根式,即可得到结果;
②在直角三角形ABC中,由AB与BC的长,利用勾股定理求出AC的长,再由三角形的面积等于两直角边乘积的一半来求,也利用由斜边乘以斜边上的高来求,即可求出斜边上的高;
③将所求式子第一项分子分解因式,第二项分母提取a分解因式,分子被开方数利用完全平方公式及二次根式的化简公式化简,约分得到最简结果,将a的值代入化简后式子中计算,即可求出值.
点评:此题考查了二次根式的化简求值,勾股定理,负指数公式,分母有理化,完全平方公式,以及二次根式的化简公式,熟练掌握公式及定理是解本题的关键.
 +
+ =1+
=1+ ;
;②在Rt△ABC中,AB=
 ,BC=2,
,BC=2,根据勾股定理得:AC=
 =2,
=2,∵CD⊥AB,
∴S△ABC=
 AC•BC=
AC•BC= AB•CD,
AB•CD,∴CD=
 =
=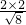 =
= ;
;③∵a=
 =
=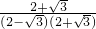 =2+
=2+ ,即a-1=2+
,即a-1=2+ -1=1+
-1=1+ >0,
>0,原式=
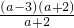 -
-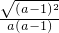 =a-3-
=a-3- =a-3-
=a-3- =2+
=2+ -3-2-
-3-2- =1.
=1.分析:①原式第一项利用负指数公式化简,第二项先判断正负,再利用绝对值的代数意义化简,最后一项化为最简二次根式,即可得到结果;
②在直角三角形ABC中,由AB与BC的长,利用勾股定理求出AC的长,再由三角形的面积等于两直角边乘积的一半来求,也利用由斜边乘以斜边上的高来求,即可求出斜边上的高;
③将所求式子第一项分子分解因式,第二项分母提取a分解因式,分子被开方数利用完全平方公式及二次根式的化简公式化简,约分得到最简结果,将a的值代入化简后式子中计算,即可求出值.
点评:此题考查了二次根式的化简求值,勾股定理,负指数公式,分母有理化,完全平方公式,以及二次根式的化简公式,熟练掌握公式及定理是解本题的关键.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目


 作图与几何计算.
作图与几何计算.