��Ŀ����
����Ŀ��ƽ��ֱ������ϵ�У�������y=ax2+bx+c��x����A��B���㣨��A�ڵ�B��ࣩ����y�ύ�ڵ�C����A��C������ֱ�Ϊ��-3��0������0��3�����Գ���ֱ��x=-1��x���ڵ�E����DΪ���㣮
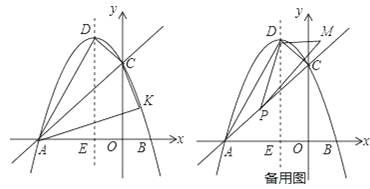
��1���������ߵĽ���ʽ��
��2����K��ֱ��AC�·�����������һ�㣬��S��KAC=S��DAC���K�����ꣻ
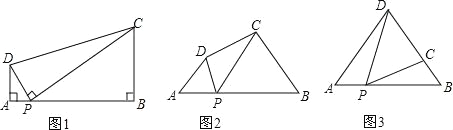
��3����ͼ2����P���߶�AC�ϵ�һ�����㣬��DPM=30�㣬DP��DM�����P���߶�AC���˶�ʱ��D�㲻�䣬M����֮�˶�����P�ӵ�A�˶�����Cʱ����M�˶���·������
���𰸡���1��y=-x2-2x+3����2����K������Ϊ��![]() ��
��![]() ����
����![]() ��
��![]() ����(3)
����(3) ![]() ��
��
��������
�����������1�����������ɵõ�����a��b��c����Ԫһ�η����飬ֻ������������Ϳɽ�����⣻
��2������D��DH��y����H������EK��y����F������EC����ͼ1�����ø���������DAC���������S��ADC=S��AEC����S��KAC=S��DAC���ɵ�S��KAC=S��EAC���Ӷ��ɵ�EK��AC������ƽ���߷��߶γɱ��������OF��Ȼ�����ô���ϵ���������ֱ��EK�Ľ���ʽ��ֻ�����ֱ��EK�������ߵĽ�������Ϳɽ�����⣻
��3�����P�ڵ�A��ʱ��M�ڵ�M�䣬��P�ڵ�C��ʱ��M�ڵ�M�壬��ͼ2����֤��DPC�ס�DMM�壬��DAC�ס�DM��M�壬�Ӷ��ɵ���DM��M=��DM��M��=��DCP��������DCP�Ƕ�ֵ����˵�M���˶�·�����߶�M��M�壬Ȼ��ֻ�������DM��M���ס�DAC���������������ε����ʾͿɽ�����⣮
�����������1��������ɵã�
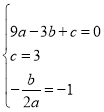 ���
���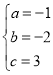 ��
��
�������ߵĽ���ʽΪy=-x2-2x+3��
��2������D��DH��y����H������EK��y����F������EC����ͼ1��

��y=-x2-2x+3=-��x+1��2+4�ɵö���DΪ��-1��4����
��S��ADC=S����AOHD-S��OAC-S��DHC
=![]() ��1+3����4-
��1+3����4-![]() ��3��3-
��3��3-![]() ��1����4-3��=3��
��1����4-3��=3��
����S��AEC=![]() AE
AE![]() OC=
OC=![]() ��2��3=3��
��2��3=3��
��S��ADC=S��AEC��
��S��KAC=S��DAC��
��S��KAC=S��EAC��
��EK��AC��
��![]() ��
��
��![]() ��
��
��OF=1��F��0��1����
��ֱ��EK�Ľ���ʽΪy=mx+n������![]() ��
��
���![]() ��
��
��ֱ��EK�Ľ���ʽΪy=x+1��
�ⷽ����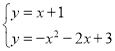 ����
���� ��
��
����K��������![]() ��
��![]() ����
����![]() ��
��![]() ����
����
��3�����P�ڵ�A��ʱ��M�ڵ�M�䣬��P�ڵ�C��ʱ��M�ڵ�M�壬��ͼ2��

�ߡ�CDM��=��PDM=90�㣬��DPM=��DCM��=30�㣬
��![]() ����PDC=��MDM�壬
����PDC=��MDM�壬
���DPC�ס�DMM�壬
���DCP=��DM��M��
ͬ���ɵ���DAC�ס�DM��M�壬
���DCA=��DM��M�䣮
���DM��M=��DM��M��=��DCP��
�ߡ�DCP�Ƕ�ֵ��
����M���˶�·�����߶�M��M�壮
�ߡ�DM��M���ס�DAC��
��![]() ��
��
��AC=![]() ��
��
��M��M��=![]() ��
��
����M���˶�·����Ϊ![]() ��
��