题目内容
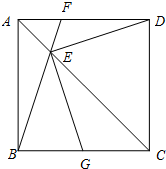 点E为正方形ABCD的对角线上一点,连接DE,BE并延长交AD于点F,EG⊥DE交BC于G,下列结论:①△BEC≌△DEC;②∠BED=120°时,EF平分∠AED; ③BG=
点E为正方形ABCD的对角线上一点,连接DE,BE并延长交AD于点F,EG⊥DE交BC于G,下列结论:①△BEC≌△DEC;②∠BED=120°时,EF平分∠AED; ③BG=| 2 |
分析:根据正方形的性质得CB=CD,∠BCE=∠DCE=45°,根据三角形全等的判定易证得△BEC≌△DEC,则可判断①正确;∠BEC=∠DEC,当∠BED=120°时,则∠DEC=60°,∠DEF=180°-120°=60°,易得∠AEF=180°-∠DEF-∠DEC=180°-60°-60°=60°,即可判断EF平分∠AED,所以②正确;过E作MN∥AB交正方形于M、N,PQ∥AD交正方形于P、Q,四边形ENCQ、四边形APEM都为正方形,由EG⊥DE得∠DEQ=∠GEN,易证得Rt△DEQ≌Rt△GEN,得到△DEQ≌△GEN,则EG=ED,由①可得ED=EB,则EB=EG,利用等腰三角形的性质得到BN=GN,则BN=AM,而AE=
AM,AM=
AE,易得BG=2BN=2AM=
AE,可判断③正确;当G点为BC的中点,设正方形ABCD的边长为4a,则BN=NG=a,NC=EN=3a,易证得Rt△MFE∽Rt△NEG,得到MF:NG=ME:EN,即MF:a=a:3a,求出MF=
a,则AF=a+
a=
a,DF=4a-
a=
a,可判断④正确.
| 2 |
| ||
| 2 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 8 |
| 3 |
解答:解:∵四边形ABCD为正方形,
∴CB=CD,∠BCE=∠DCE=45°,
在△BEC和△DEC中
DCE,
∴△BEC≌△DEC,所以①正确;
∴∠BEC=∠DEC,
当∠BED=120°时,
∴∠DEC=60°,∠DEF=180°-120°=60°,
∴∠AEF=180°-∠DEF-∠DEC=180°-60°-60°=60°,
∴∠AEF=∠DEF,即EF平分∠AED,所以②正确;
如图,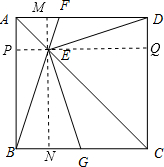 过E作MN∥AB交正方形于M、N,PQ∥AD交正方形于P、Q,
过E作MN∥AB交正方形于M、N,PQ∥AD交正方形于P、Q,
∴四边形ENCQ、四边形APEM都为正方形,
∵EG⊥DE,
∴∠DEQ=∠GEN,
在△DEQ和△GEN中,
,
∴△DEQ≌△GEN,
∴EG=ED,
∵△BEC≌△DEC,
∴ED=EB,
∴EB=EG,
∴BN=GN,
∵BN=AM,而AE=
AM,
∴AM=
AE,
∴BG=2BN=2AM=
AE,所以③正确;
当G点为BC的中点,设正方形ABCD的边长为4a,则BN=NG=a,NC=EN=3a,
∴AM=ME=a,
易证得Rt△MFE∽Rt△NEG,
∴MF:NG=ME:EN,即MF:a=a:3a,
∴MF=
a,
∴AF=a+
a=
a,
∴DF=4a-
a=
a,
∴DF=2AF,所以④正确.
故选D.
∴CB=CD,∠BCE=∠DCE=45°,
在△BEC和△DEC中
|
∴△BEC≌△DEC,所以①正确;
∴∠BEC=∠DEC,
当∠BED=120°时,
∴∠DEC=60°,∠DEF=180°-120°=60°,
∴∠AEF=180°-∠DEF-∠DEC=180°-60°-60°=60°,
∴∠AEF=∠DEF,即EF平分∠AED,所以②正确;
如图,
 过E作MN∥AB交正方形于M、N,PQ∥AD交正方形于P、Q,
过E作MN∥AB交正方形于M、N,PQ∥AD交正方形于P、Q,∴四边形ENCQ、四边形APEM都为正方形,
∵EG⊥DE,
∴∠DEQ=∠GEN,
在△DEQ和△GEN中,
|
∴△DEQ≌△GEN,
∴EG=ED,
∵△BEC≌△DEC,
∴ED=EB,
∴EB=EG,
∴BN=GN,
∵BN=AM,而AE=
| 2 |
∴AM=
| ||
| 2 |
∴BG=2BN=2AM=
| 2 |
当G点为BC的中点,设正方形ABCD的边长为4a,则BN=NG=a,NC=EN=3a,
∴AM=ME=a,
易证得Rt△MFE∽Rt△NEG,
∴MF:NG=ME:EN,即MF:a=a:3a,
∴MF=
| 1 |
| 3 |
∴AF=a+
| 1 |
| 3 |
| 4 |
| 3 |
∴DF=4a-
| 4 |
| 3 |
| 8 |
| 3 |
∴DF=2AF,所以④正确.
故选D.
点评:本题考查了相似三角形的判定与性质:有两组角分别相等的两个三角形相似;相似三角形的对应边的比相等.也考查了正方形的性质以及三角形全等的判定与性质.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
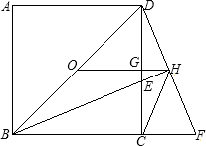 如图,点O为正方形ABCD的中心,BE平分∠DBC交DC于点E,延长BC到点F,使FC=EC,连接DF交BE的延长线于点H,连接OH交DC于点G,连接HC.则以下四个结论中正确结论的个数为( )
如图,点O为正方形ABCD的中心,BE平分∠DBC交DC于点E,延长BC到点F,使FC=EC,连接DF交BE的延长线于点H,连接OH交DC于点G,连接HC.则以下四个结论中正确结论的个数为( )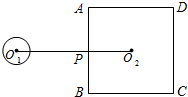 11、如图,⊙O1的半径为1,正方形ABCD的边长为6,点O2为正方形ABCD的中心,O1O2垂直AB于P点,O1O2=8.若将⊙O1绕点P按顺时针方向旋转360°,在旋转过程中,⊙O1与正方形ABCD的边只有一个公共点的情况一共出现( )
11、如图,⊙O1的半径为1,正方形ABCD的边长为6,点O2为正方形ABCD的中心,O1O2垂直AB于P点,O1O2=8.若将⊙O1绕点P按顺时针方向旋转360°,在旋转过程中,⊙O1与正方形ABCD的边只有一个公共点的情况一共出现( ) 20、如图,已知点E为正方形ABCD的边BC上一点,连接AE,过点D作DG⊥AE,垂足为G,延长DG交AB于点F.
20、如图,已知点E为正方形ABCD的边BC上一点,连接AE,过点D作DG⊥AE,垂足为G,延长DG交AB于点F.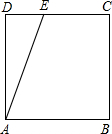 (2013•惠城区模拟)如图,点E为正方形ABCD的边CD上一点.
(2013•惠城区模拟)如图,点E为正方形ABCD的边CD上一点.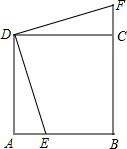 如图,点E为正方形ABCD的边CD上一点,AB=10,AE=4.△DAE旋转后能与△DCF重合.
如图,点E为正方形ABCD的边CD上一点,AB=10,AE=4.△DAE旋转后能与△DCF重合.