题目内容
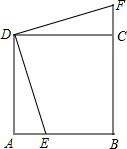 如图,点E为正方形ABCD的边CD上一点,AB=10,AE=4.△DAE旋转后能与△DCF重合.
如图,点E为正方形ABCD的边CD上一点,AB=10,AE=4.△DAE旋转后能与△DCF重合.(1)旋转中心是点
D
D
,旋转了90
90
度.(2)连接EF,则△DEF是
等腰直角
等腰直角
三角形.(3)四边形DEBF的周长和面积分别是
20+4
| 29 |
20+4
和| 29 |
100
100
.分析:(1)根据旋转变换的性质,对应边的交点是旋转中心,对应边的夹角等于旋转角,进行解答;
(2)根据旋转前后的两个图形能够完全重合,可得DE=DF,结合旋转角的度数可知是等腰直角三角形;
(3)根据勾股定理求出AE的长度,然后根据周长的定义列式计算即可求解,根据△DAE旋转后能与△DCF重合,四边形DEBF的面积等于正方形ABCD的面积,然后求解即可.
(2)根据旋转前后的两个图形能够完全重合,可得DE=DF,结合旋转角的度数可知是等腰直角三角形;
(3)根据勾股定理求出AE的长度,然后根据周长的定义列式计算即可求解,根据△DAE旋转后能与△DCF重合,四边形DEBF的面积等于正方形ABCD的面积,然后求解即可.
解答:解:(1)∵△DAE旋转后能与△DCF重合,
∴旋转中心是点D,∠ADC等于旋转角,
∵四边形ABCD是正方形,
∴∠ADC=90°,
∴旋转了90°;
(2)∵DE与DF是对应边,
∴∠EDF=90°,
∴△DEF是等腰直角三角形;
(3)∵AB=10,AE=4,
∴AD=AB=10,BE=AB-AE=10-4=6,
在Rt△ADE中,DE=
=
=2
,
∴四边形DEBF的周长=DE+BE+BF+DF=2
+6+(10+4)+2
=20+4
;
∵△DAE旋转后能与△DCF重合,
∴△DAE≌△DCF,
∴四边形DEBF的面积等于正方形ABCD的面积,
∴面积=10×10=100.
故答案为:(1)D,90;(2)等腰直角;(3)20+4
,100.
∴旋转中心是点D,∠ADC等于旋转角,
∵四边形ABCD是正方形,
∴∠ADC=90°,
∴旋转了90°;
(2)∵DE与DF是对应边,
∴∠EDF=90°,
∴△DEF是等腰直角三角形;
(3)∵AB=10,AE=4,
∴AD=AB=10,BE=AB-AE=10-4=6,
在Rt△ADE中,DE=
| AD2+AE2 |
| 102+42 |
| 29 |
∴四边形DEBF的周长=DE+BE+BF+DF=2
| 29 |
| 29 |
| 29 |
∵△DAE旋转后能与△DCF重合,
∴△DAE≌△DCF,
∴四边形DEBF的面积等于正方形ABCD的面积,
∴面积=10×10=100.
故答案为:(1)D,90;(2)等腰直角;(3)20+4
| 29 |
点评:本题考查了正方形的性质,等腰直角三角形的判定,旋转变换的性质,熟练掌握并利用旋转变换的性质是解题的关键.

练习册系列答案
相关题目
 如图,点F为正方形内一点,在正方形外有一点E,满足∠ABF=∠CBE,BF=BE.
如图,点F为正方形内一点,在正方形外有一点E,满足∠ABF=∠CBE,BF=BE.
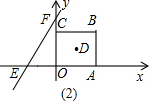

 如图,点O为正方形ABCD的中心,BE平分∠DBC交DC于点E,延长BC到点F,使FC=EC,连接DF交BE的延长线于点H,连接OH交DC于点G,连接HC.则以下四个结论中正确结论为( )
如图,点O为正方形ABCD的中心,BE平分∠DBC交DC于点E,延长BC到点F,使FC=EC,连接DF交BE的延长线于点H,连接OH交DC于点G,连接HC.则以下四个结论中正确结论为( )  如图,点F为正方形ABCD的边CD的中点,E为BC上一点,M为EF上一点,且D、M关于AF对称,B、M关于AE对称,∠CFE的平分线交AE的延长线于G,交BC于N,连CG,下列结论:①△AFG为等腰直角三角形;②CG=2
如图,点F为正方形ABCD的边CD的中点,E为BC上一点,M为EF上一点,且D、M关于AF对称,B、M关于AE对称,∠CFE的平分线交AE的延长线于G,交BC于N,连CG,下列结论:①△AFG为等腰直角三角形;②CG=2