题目内容
如图，在△ABC中，DE垂直平分BC，若AB=8，AC=6，则△ADC的周长等于（ ）| A、11 | B、13 | C、14 | D、16 |
考点：线段垂直平分线的性质
专题：
分析：由DE垂直平分BC，根据线段垂直平分线的性质，可得BD=CD，继而可得△ADC的周长等于AB+AC．
解答：解：∵DE垂直平分BC，
∴DB=DC，
∵AB=8，AC=6，
∴△ADC的周长为：AD+DC+AC=AD+BD+ACAB+AC=14．
故选C．
∴DB=DC，
∵AB=8，AC=6，
∴△ADC的周长为：AD+DC+AC=AD+BD+ACAB+AC=14．
故选C．
点评：此题考查了线段垂直平分线的性质．此题难度不大，注意掌握数形结合思想的应用．
练习册系列答案
课堂全解字词句段篇章系列答案
步步高口算题卡系列答案
点睛新教材全能解读系列答案
相关题目
下列说法中，正确的是（ ）
| A、x的系数是0 | ||
| B、5a2b的次数是2 | ||
C、-
| ||
| D、-m的系数是1 |
某部队军事训练于某日凌晨1时15分开始，部队从A地出发步行到B地，休整了1小时后，将步行速度提高下列计算错误的是（ ）
| A、（-3）2=6 | ||||||
B、-
| ||||||
| C、0-（-1）=1 | ||||||
| D、|-3|=3 |
如果a＞0，b＜0，那么下列式子一定成立的是（ ）
| A、ab＞0 | ||
B、
| ||
| C、b3＞0 | ||
| D、a-b＜0 |
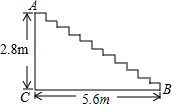某商场重新装修后，准备在大厅的主楼梯上铺设一种红色的地毯，已知这种地毯的批发价为每平方米40元，已知主楼梯道的宽为3米，其侧面如图，则买地毯至少需要多少元？