��Ŀ����
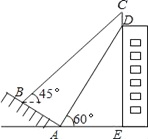
����Ŀ����ͼ��ijУһ����ѧ��¥�Ķ�������һ�顰�����������������桱��������CD��С����ɽ�µ��½�A����������Ƶײ�D������Ϊ60�㣬Ȼ����ɽ�������ߵ�B����������ƶ���C������Ϊ45�㣮��֪ɽ��AB���¶�i=1�� ![]() ��б�µ�Ǧֱ�߶���ˮƽ���ȵıȣ�����������AB=10�ף�AE=15��.
��б�µ�Ǧֱ�߶���ˮƽ���ȵıȣ�����������AB=10�ף�AE=15��.
��1�����B������ľ��룻
��2�������������CD�ĸ߶ȣ���������ĸ߶Ⱥ��Բ��ƣ�����������ţ�
���𰸡���1��5����2��������CD�ߣ�20��10![]() ��m��
��m��
�������������������1����Rt��ABH������tan��BAH=![]() =i=
=i=![]() =
=![]() ���õ���BAH=30�㣬���ǵõ����BH=ABsin��BAH=10sin30��=10��
���õ���BAH=30�㣬���ǵõ����BH=ABsin��BAH=10sin30��=10��![]() =5��
=5��
��2����Rt��ABH����AH=AB��cos��BAH=10��cos30��=5![]() ����Rt��ADE����tan��DAE=
����Rt��ADE����tan��DAE=![]() ����tan60��=
����tan60��=![]() ���õ�DE=15
���õ�DE=15![]() ����ͼ������B��BF��CE������ΪF�����BF=AH+AE=5
����ͼ������B��BF��CE������ΪF�����BF=AH+AE=5![]() +15�����ǵõ�DF=DE��EF=DE��BH=15
+15�����ǵõ�DF=DE��EF=DE��BH=15![]() ��5����Rt��BCF������C=90�㩁��CBF=90�㩁45��=45�㣬��á�C=��CBF=45�㣬�ó�CF=BF=5
��5����Rt��BCF������C=90�㩁��CBF=90�㩁45��=45�㣬��á�C=��CBF=45�㣬�ó�CF=BF=5![]() +15��������ý����
+15��������ý����
���������������1����Rt��ABH����tan��BAH=![]() =i=
=i=![]() =
=![]() �����BAH=30�㣬��BH=ABsin��BAH=10sin30��=10��
�����BAH=30�㣬��BH=ABsin��BAH=10sin30��=10��![]() =5��
=5��
������B��ˮƽ��AE�ĸ߶�BH��5����
��2����Rt��ABH����AH=AB��cos��BAH=10��cos30��=5![]() ����Rt��ADE����tan��DAE=
����Rt��ADE����tan��DAE=![]() ����tan60��=
����tan60��=![]() ����DE=15
����DE=15![]() ����ͼ������B��BF��CE������ΪF����BF=AH+AE=5
����ͼ������B��BF��CE������ΪF����BF=AH+AE=5![]() +15��DF=DE��EF=DE��BH=15
+15��DF=DE��EF=DE��BH=15![]() ��5����Rt��BCF������C=90�㩁��CBF=90�㩁45��=45�㣬���C=��CBF=45�㣬��CF=BF=5
��5����Rt��BCF������C=90�㩁��CBF=90�㩁45��=45�㣬���C=��CBF=45�㣬��CF=BF=5![]() +15����CD=CF��DF=5
+15����CD=CF��DF=5![]() +15����15
+15����15![]() ��5��=20��10
��5��=20��10![]() ���ף������������CD�ĸ߶�ԼΪ��20��10
���ף������������CD�ĸ߶�ԼΪ��20��10![]() ���ף�
���ף�


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�