Question

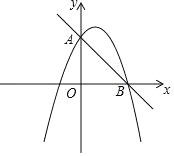
【题目】已知抛物线过点A(m-2，n)， B（m+4，n），C（m，）．

（1）b=__________（用含m的代数式表示）；

（2）求△ABC的面积；

（3）当时，均有，求m的值．

Answer 1

【答案】（1）b=-2m-2；（2）24；（3）．

【解析】

（1）根据A(m-2，n)， B（m+4，n）纵坐标一致，结合对称轴即可求解；

（2）先用含m的代数式表示c，再带入A点坐标即可求出n=3，最后利用铅锤法即可求出△ABC的面积；

（3）先用只含m的代数式表示二次函数解析式，再结合带取值范围的二次函数最值求法分类讨论即可．

（1）∵过点A(m-2，n)， B（m+4，n），

∴对称轴

∴

(2)∵

∴

把C（m，）代入

∴

∴

把A(m-2，n)代入

得

∴n=3

∴A(m-2，3)， B（m+4，3），C（m，）

∴AB=6

C点到x轴的距离为：3﹣(-5)=8，

∴S△ABC=×6×8=24

(3)∵n=3

∴

∴

∴当时

∵

∴由函数增减性知

即

∴当时

由函数增减性知时，

∴

∴（舍）

当时

由函数增减性知时，

∴

∴（舍）

∴