题目内容
如图,过原点O的直线AB与反比例函数y= (k>0)的图象交于A、B两点,点B坐标为(﹣2,m),过点A作AC⊥y轴于点C,OA的垂直平分线DE交OC于点D,交AB于点E.若△ACD的周长为5,则k的值为 .
(k>0)的图象交于A、B两点,点B坐标为(﹣2,m),过点A作AC⊥y轴于点C,OA的垂直平分线DE交OC于点D,交AB于点E.若△ACD的周长为5,则k的值为 .

6: 解:∵过原点O的直线AB与反比例函数y= (k>0)的图象交于A、B两点,
(k>0)的图象交于A、B两点,
∴A、B两点关于原点对称,
∵点B坐标为(﹣2,m),
∴点A坐标为(2,﹣m),
∵AC⊥y轴于点C,
∴AC=2,
∵DE垂直平分AO,
∴AD=OD,
∵△ACD的周长为5,
∴AD+CD=5﹣AC=3,
∴OC=AD+CD=3,
∴A(2,3),
∵点A在反比例函数y= (k>0)的图象上,
(k>0)的图象上,
∴k=2×3=6,
故答案为:6.

点评:  本题考查了一次函数与反比例函数的交点问题,线段的垂直平分线的性质,三角形的周长,得出OC=AD+CD是解题的关键.
本题考查了一次函数与反比例函数的交点问题,线段的垂直平分线的性质,三角形的周长,得出OC=AD+CD是解题的关键.

练习册系列答案
相关题目




 ),B(1,
),B(1,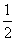 ),C(2,
),C(2, ),则此函数的最小值是
),则此函数的最小值是