题目内容
如图，A、B、E是同一直线上的三个点，四边形ABCD，BEFG都是正方形，连接AG、CE．观察图形，指出AG与CE的关系，并证明你的结论．
答：AG=CE且AG⊥CE．…
证明：∵四边形ABCD与四边形BEFG都是正方形，
∴AB=BC，BG=BE，又∠ABC=∠CBE=90°，
∴△ABG≌△CBE．…
∴AG=CE．…
∵A、B、E是同一直线上的三个点，
∴可以把△ABG绕点B顺时针旋转90°到△CBE，
由旋转的性质知AG和CE的夹角等于旋转角，即等于90°，
∴AG⊥CE．…
∴AG=CE且AG⊥CE．…
说明：只得到AG=CE且证明正确给．
分析：根据正方形的性质，利用旋转的观点，可证明△ABG≌△CBE，得出AG=CE，再利用互余关系证明AG⊥CE．
点评：本题考查了全等三角形的判定与性质．关键是利用旋转的性质找出全等三角形，利用全等三角形的性质证题．
证明：∵四边形ABCD与四边形BEFG都是正方形，
∴AB=BC，BG=BE，又∠ABC=∠CBE=90°，
∴△ABG≌△CBE．…
∴AG=CE．…
∵A、B、E是同一直线上的三个点，
∴可以把△ABG绕点B顺时针旋转90°到△CBE，
由旋转的性质知AG和CE的夹角等于旋转角，即等于90°，
∴AG⊥CE．…
∴AG=CE且AG⊥CE．…
说明：只得到AG=CE且证明正确给．
分析：根据正方形的性质，利用旋转的观点，可证明△ABG≌△CBE，得出AG=CE，再利用互余关系证明AG⊥CE．
点评：本题考查了全等三角形的判定与性质．关键是利用旋转的性质找出全等三角形，利用全等三角形的性质证题．
练习册系列答案
小学生10分钟口算测试100分系列答案
相关题目
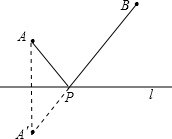几何模型：条件：如图，A、B是直线l同旁的两个定点．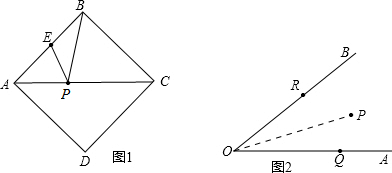
8、如图所示，∠A与∠B是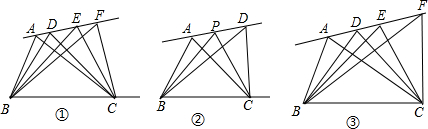
如图所示，∠1和∠3是直线
（n表示的正整数）时，S△ABC=6n，S△DBC=n（n+5），求S△PBC