题目内容
如图①,△ABC,△DBC,△EBC,△FBC…有公共边BC,而顶点A,D,E,F…都在一条直线上,我们规定这样的三角形叫同底共线的三角形.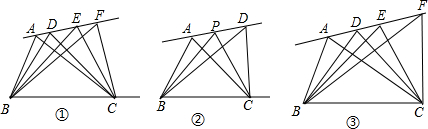
(1)如图②,△ABC,△PBC,△DBC是同底共线三角形,若PD=2PA,△DOC的面积与△AOB的面积的差为3,△PBC的面积为5,求△DBC和△ABC的面积.
(2)如图②,当AP=
| 1 | n |
(3)如图③,在同底共线三角形△ABC,△DBC,△EBC,△FBC中,若满足AD:DE:EF=a:b:c,求△ABC,△DBC,△EBC,△FBC之间的关系.
分析:(1)小题分别作△ABC,△PBC,△DBC的高线AE,PF,DG,过A作底边BC的平行线,利用三角形的面积公式即可求出△DBC和△ABC的面积;
(2)先由已知得出PM=
DN,并求出△DBC的面积与△ABC的面积的差,再利用面积公式即可求出△PBC的面积;
(3)小题设△ABC的面积是s1=x,△EBC的面积是s3=y,△DBC的面积是s2,△FBC的面积是s4,把x、y当作已知,与(2)求法类似求出s3和s4,并计算出s4-s2 和s3-s1的值,即可求出△ABC,△DBC,△EBC,△FBC之间的关系.
(2)先由已知得出PM=
| 1 |
| n |
(3)小题设△ABC的面积是s1=x,△EBC的面积是s3=y,△DBC的面积是s2,△FBC的面积是s4,把x、y当作已知,与(2)求法类似求出s3和s4,并计算出s4-s2 和s3-s1的值,即可求出△ABC,△DBC,△EBC,△FBC之间的关系.
解答: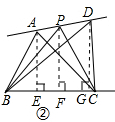 解:(1)分别作△ABC,△PBC,△DBC的高线AE,PF,DG,过A作底边BC的平行线,交PF于M,交DG于N,则四边形AEGN是矩形.
解:(1)分别作△ABC,△PBC,△DBC的高线AE,PF,DG,过A作底边BC的平行线,交PF于M,交DG于N,则四边形AEGN是矩形.
在△DAN中,∵PM∥DN,
∴PM:DN=AP:AD=1:3,∴DN=3PM.
∵S△DOC-S△AOB=3,
∴S△DBC-S△ABC=3,
∴
•BC•DG-
•BC•AE=3,
∴
•BC•DN=3,
∴
•BC•3PM=3,
∴
•BC•PM=1.
又∵S△PBC=5,
∴
•BC•(PM+MF)=5,
∴
•BC•PM+
•BC•MF=5,
∴
•BC•MF=5-1=4,
∴S△ABC=
•BC•AE=
•BC•MF=4,S△DBC=3+S△ABC=7.
(2)解:由(1)知:
=
,
∵AP=
AD,
∴
=
,
∴PM=
DN,
∵S△ABC=6n,S△DBC=n(n+5),
设△ABC的面积是s1,△DBC的面积是s3,△PBC的面积是s2,
则s3-s1=n2-n,
即
•BC•DG-
•BC•AR=n2-n,
∴
•BC•DN=n2-n,
∴s2=
•BC•PF,
=
•BC•(PM+MF),
=
•BC•PM+
•BC•MF,
∵AE=MF,PM=
DN,
∴s2=
•BC•
DN+
•BC•AE,
=
(n2-n)+6n
=7n-1.
故△PBC的面积是7n-1.
(3)解:设△ABC的面积是s1=x,△EBC的面积是s3=y,△DBC的面积是s2,△FBC的面积是s4,
过F做FH⊥BC交于H,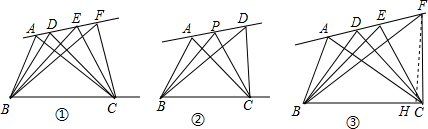
与(2)同法可求:FQ=
EN,s2=
(y-x)+x,
s4=
•BC•FH=
•BC•(FQ+AE),
=
BC•PQ+
BC•AE,
=
(y-x)+x,
∵s3-s1=y-x,
s4-s2=
(y-x),
s4-s2=
(s3-s1).
故△ABC,△DBC,△EBC,△FBC之间的关系是s△FBC-s△DBC=
(s△EBC-s△ABC).
 解:(1)分别作△ABC,△PBC,△DBC的高线AE,PF,DG,过A作底边BC的平行线,交PF于M,交DG于N,则四边形AEGN是矩形.
解:(1)分别作△ABC,△PBC,△DBC的高线AE,PF,DG,过A作底边BC的平行线,交PF于M,交DG于N,则四边形AEGN是矩形.在△DAN中,∵PM∥DN,
∴PM:DN=AP:AD=1:3,∴DN=3PM.
∵S△DOC-S△AOB=3,
∴S△DBC-S△ABC=3,
∴
| 1 |
| 2 |
| 1 |
| 2 |
∴
| 1 |
| 2 |
∴
| 1 |
| 2 |
∴
| 1 |
| 2 |
又∵S△PBC=5,
∴
| 1 |
| 2 |
∴
| 1 |
| 2 |
| 1 |
| 2 |
∴
| 1 |
| 2 |
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
(2)解:由(1)知:
| PM |
| DN |
| AP |
| AD |
∵AP=
| 1 |
| n |
∴
| PM |
| DN |
| 1 |
| n |
∴PM=
| 1 |
| n |

∵S△ABC=6n,S△DBC=n(n+5),
设△ABC的面积是s1,△DBC的面积是s3,△PBC的面积是s2,
则s3-s1=n2-n,
即
| 1 |
| 2 |
| 1 |
| 2 |
∴
| 1 |
| 2 |
∴s2=
| 1 |
| 2 |
=
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
∵AE=MF,PM=
| 1 |
| n |
∴s2=
| 1 |
| 2 |
| 1 |
| n |
| 1 |
| 2 |
=
| 1 |
| n |
=7n-1.
故△PBC的面积是7n-1.
(3)解:设△ABC的面积是s1=x,△EBC的面积是s3=y,△DBC的面积是s2,△FBC的面积是s4,
过F做FH⊥BC交于H,

与(2)同法可求:FQ=
| a+b+c |
| a+b |
| a |
| a+b |
s4=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
=
| a+b+c |
| a+b |
∵s3-s1=y-x,
s4-s2=
| b+c |
| a+b |
s4-s2=
| b+c |
| a+b |
故△ABC,△DBC,△EBC,△FBC之间的关系是s△FBC-s△DBC=
| b+c |
| a+b |
点评:解此题的关键是巧妙地利用三角形的面积公式,用到的知识点是三角形的面积公式,矩形的性质,平行线分线段成比例定理.难度较大.

练习册系列答案
相关题目

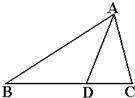 20、如图,在△ABC中,∠B=42°,∠C=72°,AD是△ABC的角平分线,
20、如图,在△ABC中,∠B=42°,∠C=72°,AD是△ABC的角平分线, 8、如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE的外部时,则∠A与∠1和∠2之间有一种数量关系始终保持不变,请试着找一找这个规律,你发现的规律是( )
8、如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE的外部时,则∠A与∠1和∠2之间有一种数量关系始终保持不变,请试着找一找这个规律,你发现的规律是( )