题目内容
15．在Rt△ABC中，∠C=90°，点G是Rt△ABC的重心，如果CG=6，那么斜边AB的长等于18．分析 CD为斜边上的中线，如图，根据重心的性质得到DG=$\frac{1}{2}$CG=3，则CD=9，然后根据直角三角形斜边上的中线性质即可得到AB的长．
解答 解：
CD为斜边上的中线，如图，
∵点G是Rt△ABC的重心，
∴CG：GD=2：1，
∴DG=$\frac{1}{2}$CG=$\frac{1}{2}$×6=3，
∴CD=3+6=9，
∴AB=2CD=18．
故答案为18．
点评 本题考查了三角形重心：三角形的重心是三角形三边中线的交点．重心到顶点的距离与重心到对边中点的距离之比为2：1．也考查了直角三角形斜边上的中线性质．
练习册系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
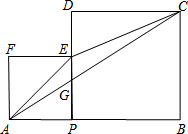如图，AB=a，P是线段AB上任意一点（点P不与A、B重合），分别以AP，BP为边作正方形APEF、正方形PBCD，点E在边PD上．设AP=x．
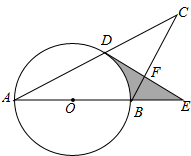如图，在△ABC中，AB=BC，以AB为直径的⊙O与AC交于点D，过点D作⊙O的切线DE，分别交BC，AB的延长线于点F，E．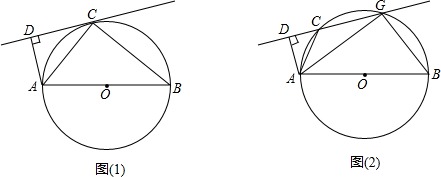
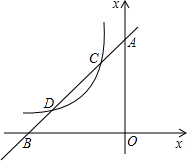7．如果把分式$\frac{ab}{a-b}$中的a、b都扩大到原来的2倍，那么分式的值是原分式值的（ ）
| A． | 4倍 | B． | 3倍 | C． | 2倍 | D． | 1倍 |
如图，直线y1=x+m，分别与x轴、y轴交于点A、B，与双曲线y2=（x＜0）的图象相交于点C、D，其中（-1，2）．