题目内容
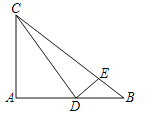
【题目】在Rt△ABC中,∠A=90°,AB=4,AC=3,D为AB边上一动点(点D与点A、B不重合),联结CD,过点D作DE⊥DC交边BC于点E.
(1)如图,当ED=EB时,求AD的长;
(2)设AD=x,BE=y,求y关于x的函数解析式并写出函数定义域;
(3)把△BCD沿直线CD翻折得△CDB',联结AB',当△CAB'是等腰三角形时,直接写出AD的长.
【答案】(1)AD=![]() ;(2)y=
;(2)y=![]() (0<x<4);(3)
(0<x<4);(3)![]() ﹣
﹣![]() 或
或![]() +
+![]()
【解析】
(1)根据等角的余角相等,证明∠ACD=∠EDB=∠B,推出tan∠ACD=tan∠B,得到![]() 即可求出AD;
即可求出AD;
(2)求出sin∠B=![]() ,cos∠B=
,cos∠B=![]() ,表达出EH,BH,DH,证明△ACD∽△HDE,利用相似比即可解答;
,表达出EH,BH,DH,证明△ACD∽△HDE,利用相似比即可解答;
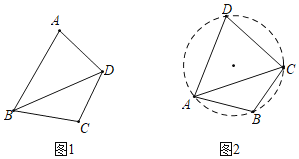
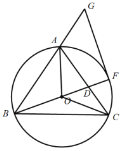
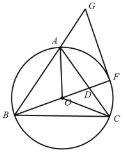
(3)分两种情形:①如图31中,设CB′交AB于K,作AE⊥CK于E,DM⊥CB′于M,DN⊥BC于N.利用角平分线的性质定理求出BD即可.②如图32中,当CB′交BA的延长线于K时,同法可得BD.
解:(1)∵ED=EB,
∴∠EDB=∠B,
∵CD⊥DE,
∴∠CDE=∠A=90°,
∵∠ACD+∠ADC=90°,∠ADC+∠EDH=90°,
∴∠ACD=∠EDB=∠B,
∴tan∠ACD=tan∠B,
∴![]() ,
,
∴![]() ,
,
∴AD=![]() .
.
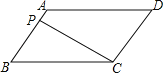
(2)如图1中,作EH⊥BD于H.
在Rt△ACB中,
∵∠A=90°,AC=3,AB=4,
∴BC=![]() ,
,
∴sin∠B=![]() ,cos∠B=
,cos∠B=![]()
∵BE=y,
∴EH=BEsin∠B =![]() y,BH=BEcos∠B =
y,BH=BEcos∠B =![]() y,
y,
∴DH=AB﹣AD﹣BH=4﹣x﹣![]() y,
y,
∵∠A=∠DHE=90°,∠ACD=∠EDH,
∴△ACD∽△HDE,
∴![]() ,
,
∴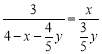 ,
,
∴y=![]() (0<x<4).
(0<x<4).
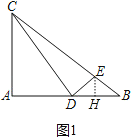
(3)①如图3﹣1中,设CB′交AB于K,作AE⊥CK于E,DM⊥CB′于M,DN⊥BC于N

∵AC=AB=3,AE⊥CB′,
∴CE=E B′=![]() CB′=
CB′=![]() ,
,
∴AE=![]() ,
,
∵∠ACE=∠KCA,∠AEC=∠KAC=90°,
∴△ACE∽△KCA,
∴![]() ,即
,即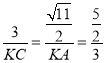
∴AK=![]() ,CK=
,CK=![]() ,
,
∴BK=AB﹣AK=4﹣![]() ,
,
∵∠DCK=∠DCB,DM⊥CM,DN⊥CB,
∴DM=DN,
∴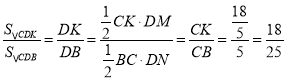 ,
,
∴BD=![]() BK=
BK=![]() ﹣
﹣![]() ,
,
∴AD=AB﹣BD=4﹣(![]() ﹣
﹣![]() )=
)=![]() +
+![]() .
.
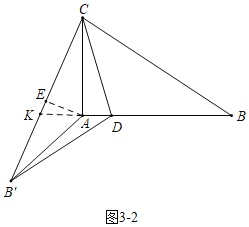
②如图3﹣2中,当CB′交BA的延长线于K时,同法可得BD=![]() BK==
BK==![]() +
+![]() ,
,
∴AD=AB﹣BD=![]() ﹣
﹣![]() .
.

 教材全解字词句篇系列答案
教材全解字词句篇系列答案