Question

【题目】如图，在中，、两点分别在边、上，，与相交于点，若的面积为，则的面积为________．

Answer 1

【答案】6

【解析】

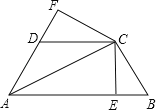
过点D作DG//BE交AC于点G，根据等高的两个三角形底边的关系，可得两个三角形面积的关系，根据相似三角形判定与性质，可得AE：EG=AF：FD=3：4，根据比例的性质，可得AF：AD=3：7，再根据等高的两个三角形底边的关系，可得两个三角形面积的关系．

过点D作DG//BE交AC于点G，

∵AE：EC=CD：BD=1：2，△ABC的面积为21，

∴S△ABE：S△BCE=S△ADC：S△ABD=1：2，

∴S△ABD＝S△ABC=×21=14，

∵DG∥BE，

∴△CDG∽△CBE，△AEF∽△AGD，

∴，

GE=CE，AE=CE，

∴AE：EG=AF：FD=3：4，

∴AF：AD=3：7，

∴S△ABF：S△ABD=3：7，

∴S△ABF=S△ABD=×14=6，

故答案为：6．