题目内容
如图,在□ABCD中,AB∶AD=3∶2,∠ADB=60°,那么cosA的值等于( )


A. | B. | C. | D. |
A.
试题分析:设AD=2x,则AB=3x,过点D作DE⊥AB于点E,过点A作AF⊥DB于点F,因为∠ADB=60°,所以DF=x,AF=
 x,在△ABF中,BF=
x,在△ABF中,BF= x,根据三角形的面积公式S=
x,根据三角形的面积公式S= BD×AF=
BD×AF= AB×DE,所以有DE=
AB×DE,所以有DE= x,在△ADE中,由勾股定理得AE=
x,在△ADE中,由勾股定理得AE= x,所以cos∠DAB=
x,所以cos∠DAB= ,故选A.
,故选A.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 .
.
 CB,过程如下:过点C作CE⊥CB于点C,与MN交于点E
CB,过程如下:过点C作CE⊥CB于点C,与MN交于点E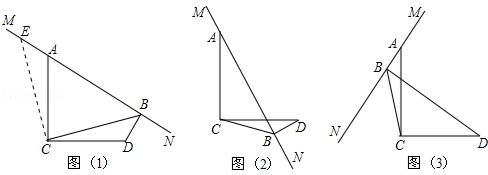
 ,求
,求 的值.
的值. 是锐角△ABC的三个内角,且满足
是锐角△ABC的三个内角,且满足 ,求
,求 的度数.
的度数.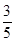 ,则
,则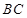 的长是( )
的长是( ) .
.