Question

如图，是地下排水管的截面图（圆形），小敏为了计算地下排水管的直径，在圆形弧上取了A，B两点并连接AB，在劣弧AB上取中点C连接CB，经测量米，∠ABC=36.87°，根据这些数据请你计算出地下排水管的直径（精确到0.1米）（sin36.87°≈0.60，cos36.87°≈0.80，tan36.87°≈0.75）．

Answer 1

解：设圆心为O，连接BO、CO交AB于D，
∵C是弧AB的中点，CO是半径，
∴AD=BD，CO⊥AB．
在Rt△BCD中BC=米，∠ABC=36.87°，
∴CD=BCsin∠ABC=sin36.87°=，
BD=BCcos∠ABC=cos36.87°=1，
在Rt△BOD中，设圆的半径为x，
DO²+BD²=BO²，
（x-）²+1²=x²，
x=，
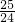2x=≈2.1（米）．
答：地下排水管的直径约为2.1米．
分析：连接BO、CO，根据垂径定理和三角函数求出CD的长，再勾股定理求出圆的半径即可．
点评：此题考查了垂径定理的应用，连接BO、CO，构造直角三角形是解题的关键．由实际问题抽象出垂径定理是解题的关键．