Question

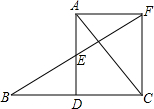如图，△ABC中，D是BC边上的一点，E是AD的中点，过点A作BC的平行线交BE的延长线于F，且AF=DC，连接CF．
（1）求证：D是BC的中点；
（2）如果AB=AC，试猜想四边形ADCF的形状，并证明你的结论；
（3）△ABC满足什么条件时四边形ADCF为正方形，并证明你的结论．

Answer 1

分析：（1）首先利用平行线的性质得出△AEF≌△DEB，进而得出D为BC的中点；
（2）利用等腰三角形的性质以及矩形的判定得出即可；
（3）当△ABC为等腰直角三角形时，利用正方形的判定得出四边形ADCF为正方形即可．

解答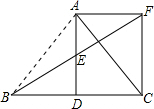：证明：
（1）∵AF=DC，AF∥BC，∴四边形AFCD为平行四边形，∴AF=CD
又∵E为AD的中点，AF∥BD，∴AE=DE，∠AFE=∠DBE，
在△AEF和△DEB中

∠AEF=∠BED ∠AFE=∠DBE AF=CD

∴△AEF≌△DEB（AAS），
∴BD=AF，∴BD=CD，
即D为BC的中点；

（2）四边形ADCF为矩形；
理由：连接AB，
∵AB=AC，D为BC的中点，
∴AD⊥BC，∴∠ADC=90°
∴平行四边形AFCD为矩形；

（3）当△ABC为等腰直角三角形时，四边形ADCF为正方形；
理由：∵△ABC为等腰直角三角形，D为BC中点，
∴AD⊥BC，AD=

1

2

BC=BD=CD，
∴平行四边形ADCF为矩形，
∴矩形ADCF为正方形．

点评：此题主要考查了矩形的判定和正方形的判定和全等三角形的判定等知识，熟练区分矩形与正方形是解题关键．