题目内容
已知△ABC,
(1)如图l,若P点是 ABC和
ABC和 ACB的角平分线的交点,则
ACB的角平分线的交点,则 P=
P= ;
;
(2)如图2,若P点是 ABC和外角
ABC和外角 ACE的角平分线的交点,则
ACE的角平分线的交点,则 P=
P=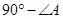 ;
;
(3)如图3,若P点是外角 CBF和
CBF和 BCE的角平分线的交点,则
BCE的角平分线的交点,则 P=
P=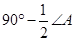 。
。
上述说法正确的个数是( )
| A.0个 | B.1个 | C.2个 | D.3个 |
C
解析该试题考查知识点:三角形的内角和定理、外角、角平分线
思路分析:利用角平分线的定义、三角形的内角和定理进行演算
具体解答过程:
(1)、对图1来说:
∵P点是 ABC和
ABC和 ACB的角平分线的交点
ACB的角平分线的交点
∴ PBC=
PBC=
 ABC,
ABC, PCB=
PCB=
 ACB
ACB
∵ ABC+
ABC+ ACB=180°-
ACB=180°- A
A
∴ PBC+
PBC+ PCB =
PCB =
 ABC+
ABC+
 ACB=
ACB= (
( ABC+
ABC+ ACB)=
ACB)= (180°-
(180°- A)=90°-
A)=90°-
 A
A
∴ P=180°-(
P=180°-( PBC+
PBC+ PCB)=180°-(90°-
PCB)=180°-(90°-
 A)=
A)=
(2)、对图2来说:
∵P点是 ABC和外角
ABC和外角 ACE的角平分线的交点
ACE的角平分线的交点
∴ PBC=
PBC=
 ABC,
ABC, PCA=
PCA=
 ACE
ACE
∵ ACE=
ACE= A+
A+ ABC,
ABC, BCA=180°-
BCA=180°- A-
A- ABC
ABC
∴ P=180°-
P=180°- PBC-
PBC- ACB -
ACB - PCA=180°-
PCA=180°-
 ABC-(180°-
ABC-(180°- A-
A- ABC)-
ABC)- (
( A+
A+ ABC)=
ABC)=
 A
A
(3)、对于图3来说:
∵P点是外角 CBF和
CBF和 BCE的角平分线的交点
BCE的角平分线的交点
∴ PBC=
PBC= ,
, PCB=
PCB=
 P=180°-
P=180°- PBC-
PBC- PCB=180°-
PCB=180°-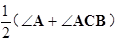 -
- =180°-
=180°- A-
A- (
( ACB+
ACB+ ABC)=180°-
ABC)=180°- A-
A- (180°-
(180°- A)=
A)=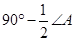
综上所述,与题中所给的说法对比可知:只有(1)和(3)两个是正确的。
故选C
试题点评:演算繁琐,需及时化简。这类题目在中考中出现的几率较小,但作为平时的练习还是有一定价值的。

练习册系列答案
相关题目
已知ABC的三边满足a2+b2+c2-ab-bc-ac=0,则这个三角形的形状是( )
| A、直角三角形 | B、等腰三角形 | C、等腰直角三角形 | D、等边三角形 |
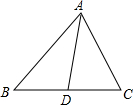 如图,已知ABC中,AD为BC边上的中线,且AB=4cm,AC=3cm,则AD的取值范围是( )
如图,已知ABC中,AD为BC边上的中线,且AB=4cm,AC=3cm,则AD的取值范围是( )| A、3<AD<4 | ||||
| B、1<AD<7 | ||||
C、
| ||||
D、
|
已知△ABC中,cosA=
,tgB=1,则△ABC的形状是( )
| 1 |
| 2 |
| A、锐角三角形 |
| B、直角三角形 |
| C、钝角三角形 |
| D、等腰三角形 |
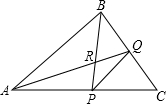 如图,已知△ABC,∠B的平分线交边AC于P,∠A的平分线交边BC于Q,如果过点P、Q、C的圆也过△ABC的内心R,且PQ=1,则PR的长等于
如图,已知△ABC,∠B的平分线交边AC于P,∠A的平分线交边BC于Q,如果过点P、Q、C的圆也过△ABC的内心R,且PQ=1,则PR的长等于